Giải SBT toán 10 kết nối Bài tập cuối chương III
Tài liệu hướng dẫn giải Toán lớp 10 Kết Nối Tri Thức của Giaibaitapsgk có đủ cả tập 1, tập 2 và được chia theo từng tuần học đảm bảo các em có thể nhanh chóng tra cứu. Dựa vào đáp án để so sánh kết quả nhận ra điểm sai trong các bước giải của mình, đồng thời cũng làm quen với các dạng toán quan trọng trong chương trình Toán lớp 10. Ngoài ra, chúng tôi cũng hỗ trợ giải vở bài tập Toán 10 theo từng trang.
Hướng dẫn giải Bài tập cuối chương III trang 40 SBT toán 10 tập 1. Đây là sách bài tập nằm trong bộ sách "Kết nối tri thức" được biên soạn theo chương trình đổi mới của Bộ giáo dục. Hi vọng, với cách hướng dẫn cụ thể và giải chi tiết học sinh sẽ nắm bài học tốt hơn.
Bài tập 3.17. Tam giác ABC có $\widehat{A} = 15^{o}$, $\widehat{B} = 45^{o}$. Giá trị của tanC bằng
A. $-\sqrt{3}$. B. $\sqrt{3}$. C. $\frac{1}{\sqrt{3}}$. D. $\frac{1}{-\sqrt{3}}$
Trả lời: Chọn đáp án: A. $-\sqrt{3}$.
$\widehat{C} = 180^{o} - \widehat{A} - \widehat{B} = 180^{o} - 15^{o} - 45^{o} = 120^{o}$
tanC = tan30 = $-\sqrt{3}$
Bài tập 3.18. Trên mặt phẳng toạ độ Oxy, lấy điểm M thuộc nửa đường tròn đơn vị sao cho $\widehat{xOM} = 35^{o}$. Tích hoành độ và tung độ của điểm M bằng
A. $\frac{1}{2\sqrt{2}}$. B. $\frac{1}{2}$. C. $\frac{-1}{2}$. D. A. -$\frac{1}{2\sqrt{2}}$.
Trả lời: Chọn đáp án: B. $\frac{1}{2}$.
$\widehat{xOM} = 135^{o}$
$\Rightarrow sin\widehat{xOM} = \frac{\sqrt{2}}{2}$
$cos\widehat{xOM} = -\frac{\sqrt{2}}{2}$
$x_{M}.y_{M} = \frac{\sqrt{2}}{2} . (-\frac{\sqrt{2}}{2}) = -\frac{1}{2}$
Bài tập 3.19. Trên mặt phẳng toạ độ Oxy, lấy điểm M thuộc nửa đường tròn đơn vị sao cho $\widehat{xOM} = 105^{o}$. N là điểm đối xứng với M qua trục tung. Giá trị của tan $\widehat{xON}$ bằng
A. $\frac{1}{\sqrt{3}}$. B. -$\frac{1}{\sqrt{3}}$. C. $\sqrt{3}$. D. -$\sqrt{3}$.
Trả lời: Chọn đáp án: A. $\frac{1}{\sqrt{3}}$.
N đối xứng với M qua trục tung ta có:
$x_{N} = - x_{M}$
$\Rightarrow cos\widehat{xON} = -cos\widehat{xOM}$
$\Rightarrow cos\widehat{xON} = 150^{o} = -(\frac{\sqrt{3}}{2}) = \frac{\sqrt{3}}{2}$
$y_{N} = y_{M}$
$\Rightarrow sin\widehat{xON} = sin\widehat{xOM}$
$\Rightarrow sin\widehat{xON} = 150^{o} = \frac{1}{2}$
$tan\widehat{xON} = \frac{sin\widehat{xON}}{cos\widehat{xON}} = \frac{1}{\sqrt{3}}$
Bài tập 3.20. Cho góc nhọn $\alpha$ có tan $\alpha = \frac{3}{4}$. Giá trị của tích sin$\alpha$ . cos$\alpha$ bằng
A. $\frac{4}{3}$. B. $\frac{12}{25}$. C. $\frac{25}{12}$. D. $\frac{3}{4}$.
Trả lời: Chọn đáp án: B. $\frac{12}{25}$.
$tan\alpha = \frac{3}{4}$
$\Rightarrow \frac{sin\alpha}{cos\alpha} = \frac{3}{4}$
$\Rightarrow sin\alpha = \frac{3}{4}cos\alpha$
Do đó $sin\alpha . cos\alpha = \frac{3}{4}cos\alpha . cos\alpha = \frac{3}{4}cos^{2}\alpha$
Mà $tan\alpha = \frac{3}{4}$
$\Rightarrow tan^{2}\alpha = \frac{9}{16}$
$\Rightarrow \frac{1}{cos^{2}\alpha} - 1 = \frac{9}{16}$
$\Rightarrow \frac{1}{cos^{2}\alpha} = \frac{25}{16}$
$\Rightarrow cos^{2}\alpha = \frac{16}{25}$
$sin\alpha . cos\alpha = \frac{12}{25}$
Bài tập 3.21. Cho góc $\alpha$ ($0^{o} < \alpha < 180^{o}$) thoả mãn sin$\alpha$ + cos$\alpha$ = 1. Giá trị của cot$\alpha$ là
A. 0. B. 1. C. -1. D. Không tồn tại.
Trả lời: Chọn đáp án: A. 0.
Bài tập 3.22. Cho góc $\alpha$ thoả mãn sin$\alpha$ + cos$\alpha$ = $\sqrt{2}$. Giá trị của tan$\alpha$ + cot$\alpha$ là
A. 1. B.-2. C. 0. D. 2.
Trả lời: Chọn đáp án: D. 2.
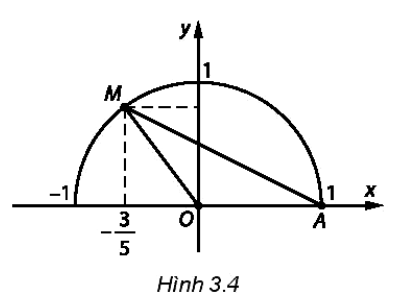
Bài tập 3.23. Trên mặt phẳng toạ độ Oxy lấy điểm y M thuộc nửa đường tròn đơn vị, sao cho $\widehat{xOM} = \frac{-3}{5}$ (H.3.4)
Diện tích của tam giác AOM bằng
A. $\frac{4}{5}$. B. $\frac{2}{5}$.
C. $\frac{3}{5}$. D. $\frac{3}{10}$.
Trả lời: Chọn đáp án: B. $\frac{2}{5}$.
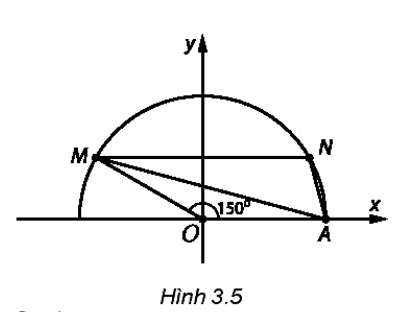
Bài tập 3.24. Trên mặt phẳng toạ độ Oxy lấy điểm M thuộc nửa đường tròn đơn vị, sao cho $\widehat{xOM} = 150^{o}$ (H.3.5). Lấy N đối xứng với M qua trục tung. Diện tích của tam giác MAN bằng
A. $\frac{\sqrt{3}}{4}$. B. $\frac{\sqrt{3}}{2}$.
C. $\sqrt{3}$ D. $2\sqrt{3}$
Trả lời: Chọn đáp án: A. $\frac{\sqrt{3}}{4}$.
Bài tập 3.25. Cho cos$\alpha = \frac{1}{4}$. Giá trị của P = $\frac{tan\alpha + 2cot\alpha}{2tan\alpha + 3cot\alpha}$
A. $\frac{-17}{33}$. B. $\frac{17}{33}$.
C. $\frac{1}{2}$. D. $\frac{16}{33}$.
Trả lời: Chọn đáp án: B. $\frac{17}{33}$.
Bài tập 3.26. Tam giác ABC có a = 2, b = 3, c = 4. Bán kính đường tròn ngoại tiếp của tam giác ABC là
A. R = $\frac{\sqrt{15}}{2}$. B. R = $\frac{7}{\sqrt{15}}$.
C. R = $\frac{\sqrt{15}}{6}$. D. R = $\frac{8}{\sqrt{15}}$.
Trả lời: Chọn đáp án: D. R = $\frac{8}{\sqrt{15}}$.
Nửa chu vi tam giác: p = $\frac{a+b+c}{2} = \frac{2+3+4}{2} = \frac{9}{2}$
Diện tích tam giác: S = $\sqrt{p(p-a)(p-b)(p-c)} = \frac{\sqrt{135}}{2}$
Bán kính đường tròn ngoại tiếp tam giác: R = $\frac{abc}{4S} = \frac{2.3.4}{4\frac{\sqrt{135}}{2}} = \frac{8}{\sqrt{15}}$
Bài tập 3.27. Tam giác ABC có a = 4, b = 5, c = 6. Độ dài đường cao $h_{b}$ bằng
A. $\frac{3\sqrt{7}}{2}$. B. $\frac{3}{2\sqrt{7}}$.
C. $\frac{3\sqrt{7}}{4}$. D. $\frac{3}{4\sqrt{7}}$.
Trả lời: Chọn đáp án: A. $\frac{3\sqrt{7}}{2}$.
Nửa chi vi tam giác: p = $\frac{a+b+c}{2} = \frac{4+5+6}{2} = \frac{15}{2}$
Diện tích tam giác: S = $\sqrt{p(p-a)(p-b)(p-c)} = \frac{15\sqrt{7}}{4}$
Áp dụng công thức: S = $\frac{1}{2}.b.h_{b}$
Suy ra $h_{b} = \frac{3\sqrt{7}}{2}$
Bài tập 3.28. Cho tam giác ABC có a = 20, b = 16 và $m_{a}$ = 10. Diện tích của tam giác bằng
A. 92. B. 100.
C. 96. D. 88.
Trả lời: Chọn đáp án: C. 96.
Áp dụng công thức tính độ dài đường trung tuyến ta có:
$m^{2}_{a} = \frac{b^{2}+c^{2}}{2} - \frac{a^{2}}{4}$
$10^{2} = \frac{16^{2}+c^{2}}{2} - \frac{20^{2}}{4}$
$\Rightarrow c^{2} = 144$
$\Rightarrow c = 12$
Áp dụng công thức nửa chu vi tam giác ta có:
$p = \frac{a+b+c}{2} = \frac{20+16+12}{2} = 24$
Diện tích tam giác là:
$S = \sqrt{p(p-a)(p-b)(p-c)} = \sqrt{24(24-20)(24-16)(24-12)} = 96$
Bài tập 3.29. Tam giác ABC có a = 14 b = 9 và $m_{a}$ = 8. Độ dài đường cao $h_{a}$ bằng
A. $\frac{24\sqrt{5}}{7}$. B. $\frac{12\sqrt{5}}{7}$.
C. $12\sqrt{5}$. D. $24\sqrt{5}$.
Trả lời: Chọn đáp án: A. $\frac{24\sqrt{5}}{7}$.
Áp dụng công thức tính độ dài đường trung tuyến ta có:
$m^{2}_{a} = \frac{b^{2}+c^{2}}{2} - \frac{a^{2}}{4}$
$8^{2} = \frac{9^{2}+c^{2}}{2} - \frac{12^{2}}{4}$
$\Rightarrow c^{2} = 145$
$\Rightarrow c = \sqrt{145}$
Áp dụng công thức nửa chu vi tam giác ta có:
$p = \frac{a+b+c}{2} = \frac{14+9+\sqrt{145}}{2} = \frac{23+\sqrt{145}}{2}$
Áp dụng diện tích tam giác ta có:
$S = \sqrt{p(p-a)(p-b)(p-c)} = 24\sqrt{5}$
Độ dài đường cao $h_{a}$ bằng
$S = \frac{1}{2}h_{a}a$ $\Rightarrow h_{a} = \frac{24\sqrt{5}}{7}$
Bài tập 3.30. Tam giác ABC có $\widehat{A} = 45^{o}$, c = 6, $\widehat{B} = 75^{o}$.
Độ dài đường cao $h_{b}$ bằng
A. $3\sqrt{2}$. B. $\frac{3}{\sqrt{2}}$.
C. $6\sqrt{2}$. D. $2\sqrt{3}$.
Trả lời: Chọn đáp án: A. $3\sqrt{2}$.
Có $\widehat{C} = 180^{o} - \widehat{A} - \widehat{B} = 180^{o} - 45^{o} - 75^{o} = 60^{o}$
Áp dụng định lí sin ta có:
$\frac{b}{sin B} = \frac{c}{sin C}$
$\Rightarrow b = \frac{c}{sin C} . sin B = \frac{6}{sin 60} . sin 75 = \sqrt{6} + 3\sqrt{2}$
Áp dụng công thức diện tích tam giác ta có:
$S = \frac{1}{2}bcsin A = \frac{1}{2}.(\sqrt{6} + 3\sqrt{2}).6.sin 45 = 9 + 3\sqrt{3}$
Ta có $S = \frac{1}{2}h_{b}b$
$\Rightarrow h_{b} = \frac{2S}{b} = \frac{2.(9 + 3\sqrt{3})}{\sqrt{6} + 3\sqrt{2}} = 3\sqrt{2}$
Bài tập 3.31. Tam giác ABC có $\widehat{A} = 45^{o}$, c = 6, $\widehat{A} = 75^{o}$.
Độ dài bán kính đường tròn ngoại tiếp của tam giác bằng
A. $8\sqrt{3}$. B. $2\sqrt{3}$.
C. $6\sqrt{3}$. D. $4\sqrt{3}$.
Trả lời: Chọn đáp án: B. $2\sqrt{3}$.
$\widehat{C} = 180^{o} - \widehat{A} - \widehat{B} = 180^{o} - 45^{o} - 75^{o} = 60^{o}$
Áp dụng định lí sin ta có:
$\frac{c}{sin C} = 2R$
$\Rightarrow R = \frac{c}{2sin C} = \frac{6}{2sin 60} = 2\sqrt{3}$
Bài tập 3.23. Tam giác ABC có diện tích S = $2R^{2}$.sinBsinC, với R là độ đài bán kính đường tròn ngoại tiếp của tam giác. Số đo góc A bằng
A. $60^{o}$. B. $90^{o}$.
C. $30^{o}$. D. $75^{o}$.
Trả lời: Chọn đáp án: B. $90^{o}$.
Áp dụng định lí sin ta có:
$\frac{a}{sin A} = \frac{b}{sin B} = \frac{c}{sin C} =2R$
$\Rightarrow$ a = 2R.sin A, b= 2R.sin B, c = 2R.sin C
Áp dụng công thức diện tích tam giác ta có:
$S = \frac{abc}{4R} = \frac{(2R.sin A)(2R.sin B)(R.sin C)}{4R} = \frac{8R^{3}.sin A.sin B.sin C}{4R}$
Theo đề bài ta có S = $2R^{2}$.sinBsinC nên sin A = 1 $\Rightarrow \widehat{A} = 90^{o}$
Bài tập 3.33. Tam giác ABC có AB = $\sqrt{5}$, AC = $\sqrt{2}$ và $\widehat{C} = 45^{o}$
Độ dài cạnh BC bằng
A. 3. B. 2.
C. $\sqrt{3}$. D. $\sqrt{2}$
Trả lời: Chọn đáp án: B. 2.
Áp dụng định lí côsin ta có:
$AB^{2} = AC^{2} + BC^{2} - 2.AC.BC.cos C$
$\Rightarrow (\sqrt{5})^{2} = (\sqrt{2})^{2} + BC^{2} - 2.\sqrt{2}.BC.cos 60$
$\Rightarrow BC^{2} - \frac{1}{2}BC - 3 = 0$
$\Rightarrow BC = 2$
Bài tập 3.34. Tam giác ABC có $\widehat{C} = 60^{o}$, AC = 2 và AB = $\sqrt{2}$.
Diện tích của tam giác ABC bằng
A. $\frac{\sqrt{3}}{2}$. B. $3\sqrt{3}$
C. $\frac{3\sqrt{3}}{2}$. D. $\sqrt{3}$
Trả lời: Chọn đáp án: C. $\frac{3\sqrt{3}}{2}$.
Áp dụng định lí côsin ta có:
$AB^{2} = AC^{2} + BC^{2} - 2.AC.BC.cos C$
$\Rightarrow (\sqrt{7})^{2} = 2^{2} + BC^{2} - 2.2.BC.cos 60$
$\Rightarrow BC^{2} - 2BC - 3 = 0$
$\Rightarrow BC = 3$
Áp dụng công thức diện tích tam giác ta có:
$S = \frac{1}{2}AC.BC.sin C = \frac{1}{2}.2.3.sin 60 = \frac{3\sqrt{3}}{2}$
Bài tập 3.35. Tam giác ABC có $\widehat{A} = 60^{o}$, AB = 3 và BC = $3\sqrt{3}$.
Độ dài bán kính đường tròn nội tiếp của tam giác ABC là
A. $\frac{3(\sqrt{3}-1)}{2}$. B. $\frac{3(\sqrt{3}+1)}{2}$.
C. $\frac{\sqrt{3}-1}{2}$. B. $\sqrt{3}-1$.
Trả lời: Chọn đáp án: A. $\frac{3(\sqrt{3}-1)}{2}$.
Áp dụng định lí côsin ta có:
$BC^{2} = AB^{2} + AC^{2} - 2.AB.AC.cos A$
$\Rightarrow (2\sqrt{3})^{2} = 3^{2} + AC^{2} - 2.3.AC.cos 60$
$\Rightarrow AC^{2} - 3AC - 18 = 0$
$\Rightarrow AC = 6$
Áp dụng công thức diện tích tam giác ta có:
$S = \frac{1}{2}AB.AC.sin A = \frac{1}{2}.3.6.sin 60 = \frac{9\sqrt{3}}{2}$
Có S = pr
$\Rightarrow r = \frac{S}{p} = \frac{\frac{9\sqrt{3}}{2}}{\frac{9+3\sqrt{3}}{2}} = \frac{3(\sqrt{3}-1)}{2}$
Bài tập 3.36. Một ca nô xuất phát từ cảng A, chạy theo hướng đông với vận tốc 60 km/h. Cùng lúc đó, một tàu cá, xuất phát từ A, chạy theo hướng $N30^{o}E$ với vận tốc 50 km/h. Sau 2 giờ, hai tàu cách nhau bao nhiêu kilômét?
A. 110 km. B. 112 km.
C. 111,4 km. D. 110,5 km.
Trả lời: Chọn đáp án: C. 111,4 km.

Theo đề bài ca nô chuyển động theo hướng đông và tàu cá chuyển động theo hướng $N30^{o}E$, ta có:
$\widehat{BAC} = 90^{o} - 30^{o} = 60^{o}$
Sau 2 giờ ca nô chạy được quãng đường AB bằng: 2.60 = 120 (km)
Sau 2 giờ tàu cá chạy được quãng đường AC bằng: 2.50 = 100 (km)
Áp dụng định lí côsin cho tam giác ABC ta có:
$BC^{2} = AB^{2} + AC^{2} -2.AB.AC.cos\widehat{BAC}$
$\Rightarrow BC^{2} = 12400$
$\Rightarrow BC \approx 111,4$
Bài tập 3.37. Một người đứng trên đài quan sát đặt ở cuối một đường đua thẳng. Ở độ cao 6 m so với mặt đường đua, tại một thời điểm người đó nhìn hai vận động viên A và B dưới các góc tương ứng là $60^{o}$ và $30^{o}$, so với phương nằm ngang (H.3.6). Khoảng cách giữa hai vận động viên A và B (làm tròn đến hàng đơn vị, theo đơn vị mét) tại thời điểm đó là
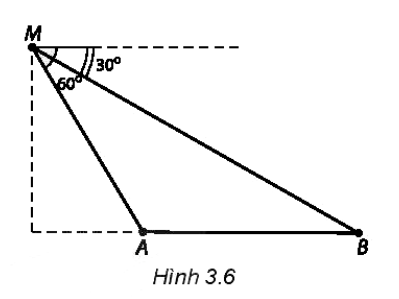
A. 8 m. B. 7 m.
C. 6 m. D. 9 m.
Trả lời: Chọn đáp án: B. 7 m.

Giả sử H là chân đài quan sát ở cuối đường đua.
Khi đó ta có: MH = 6 m
$\widehat{BMH} = 90^{o} - 30^{o} = 60^{o}$
$\widehat{AMH} = 90^{o} - 60^{o} = 30^{o}$
Tam giác AMH vuông tại H nên ta có:
HA = MH. tan $widehat{AMH}$ = 6. tan$30^{o}$ = $2\sqrt{3}$
Tương tự, tam giác BMH vuông tại H nên ta có:
HB = MH. tan $\widehat{BMH}$ = 6. tan$60^{o}$ = $6\sqrt{3}$
Độ dài đoạn AB = HB - HA = $6\sqrt{3} - 2\sqrt{3} = 4\sqrt{3}$
Vậy AB $\approx$ 7 m
Bài tập 3.38. Cho góc tù $\alpha$ có sin$\alpha = \frac{1}{3}$
a) Tính cos$\alpha$, tan$\alpha$, cot$\alpha$.
b) Tính giá trị của các biểu thức :
A = $sin\alpha . cot(180^{o} - \alpha) + cos(180^{o} - \alpha) .cot(90^{o} - \alpha)$;
B = $\frac{3(sin\alpha + \sqrt{2}cos\alpha)-2}{sin\alpha -\sqrt{2}cos\alpha}$.
Trả lời:
Có $90^{o} < \alpha < 180^{o}$ nên cos$alpha$ < 0
Áp dụng công thức:
$sin^{2}\alpha + cos^{2}\alpha = 1$
$\Rightarrow cos^{2}\alpha = 1 - sin^{2}\alpha = 1 - \frac{1}{3} = \frac{8}{9}$
$\Rightarrow cos\alpha = -\frac{2\sqrt{2}}{3}$
Áp dụng công thức:
$tan\alpha = \frac{sin\alpha}{cos\alpha} = \frac{\frac{1}{3}}{\frac{-2\sqrt{2}}{3}} = \frac{-\sqrt{2}}{4}$
$cot\alpha = \frac{cos\alpha}{sin\alpha} = \frac{\frac{-2\sqrt{2}}{3}}{\frac{1}{3}} = -2\sqrt{2}$
b) Theo công thức ta có:
$cot(180^{o} - \alpha) = -cot\alpha$
$cos(180^{o} - \alpha) = -cos\alpha$
$cot(90^{o} - \alpha) = tan\alpha$
Áp dụng vào biểu thức A = $sin\alpha . cot(180^{o} - \alpha) + cos(180^{o} - \alpha) .cot(90^{o} - \alpha)$ ta có:
A = $sin\alpha . (-cot\alpha) + (-cos\alpha) . tan\alpha$
A = $\frac{1}{3} . (-(-2\sqrt{2})) + (-(-\frac{2\sqrt{2}}{3})).(\frac{-\sqrt{2}}{4})$
A = $\frac{2\sqrt{2} - 1}{3}$
B = $\frac{3(sin\alpha + \sqrt{2}cos\alpha)-2}{sin\alpha -\sqrt{2}cos\alpha}$
B = $\frac{3(\frac{1}{3} + \sqrt{2}.(-\frac{2\sqrt{2}}{3}))-2}{\frac{1}{3} -\sqrt{2}.(-\frac{2\sqrt{2}}{3})}$
B = -3
Bài tập 3.39. Cho $sin15^{o} = \frac{\sqrt{6}-\sqrt{2}}{4}$
a) Tính $sin75^{o}$, $cos105^{o}$, $tan165^{o}$.
b) Tính giá trị của biểu thức
A = $sin75^{o} . cos165^{o} + cos165^{o} . sin165^{o}$
Trả lời:
a) Có $0^{o} < 15^{o} < 90^{o}$ nên cos$15^{o}$ > 0
Lại có $sin^{2}15^{o} + cos^{2}15^{o} = 1$
$\Rightarrow$ $cos^{2}15^{o}$ = 1 - $sin^{2}15^{o}$= 1 - $(\frac{\sqrt{6}-\sqrt{2}}{4})^{2}$ = $\frac{2+\sqrt{3}}{4}$
$\Rightarrow cos15^{o} = \frac{\sqrt{6}-\sqrt{2}}{4}$
Áp dụng công thức:
$tan15^{o} = \frac{sin15^{o}}{cos15^{o}} = \frac{\frac{\sqrt{6}-\sqrt{2}}{4}}{\frac{\sqrt{6}+\sqrt{2}}{4}} = \frac{\sqrt{6}-\sqrt{2}}{\sqrt{6}+\sqrt{2}} = \frac{(\sqrt{6}-\sqrt{2}^{})}{(\sqrt{6}+\sqrt{2})(\sqrt{6}-\sqrt{2})} = \frac{8-4\sqrt{3}}{4} = 2-\sqrt{3}$
Có $sin75^{o}$ = $sin(90^{o}-15^{o}) = cos15^{o} = \frac{\sqrt{6}+\sqrt{2}}{4}$
$cos105^{o} = cos(180^{o} - 75^{o}) = -cos75^{o} = -cos(90^{o}-15^{o}) = -sin15^{o}$
Như vậy $cos105^{o} = -\frac{\sqrt{6}-\sqrt{2}}{4}$
$tan165^{o} = tan(180^{o} - 15^{o} = -tan15^{o}$
Như vậy $tan165^{o} = -2+\sqrt{3}$
b) Có $sin165^{o} = sin(180^{o} - 15^{o}) = sin15^{o} = \frac{\sqrt{6}-\sqrt{2}}{4}$
$cos165^{o} = cos(180^{o} - 15^{o}) = -cos15^{o} = -\frac{\sqrt{6}+\sqrt{2}}{4}$
Áp dụng vào A = $sin75^{o} . cos165^{o} + cos165^{o} . sin165^{o}$
A = $\frac{\sqrt{6}+\sqrt{2}}{4}.(-\frac{\sqrt{6}+\sqrt{2}}{4})+\frac{\sqrt{2}-\sqrt{6}}{4}.\frac{\sqrt{6}-\sqrt{2}}{4}$
A = -1
Bài tập 3.40. Cho tam giác ABC có AB = 1, BC = 2 và $\widehat{ABC} = 60^{o}$. Tính độ dài cạnh và số đo các góc còn lại của tam giác.
Trả lời:
Áp dụng định lí côsin ta có:
$AC^{2} = AB^{2} + BC^{2} - 2.AB.BC.cos\widehat{ABC} = 1^{2} + 2^{2} - 2.1.2.cos\widehat{60} = 3$
$\Rightarrow AC = \sqrt{3}$
Áp dụng định lí sin ta có:
$\frac{AB}{sin\widehat{ACB}} = \frac{AC}{sin\widehat{ABC}} = \frac{BC}{sin\widehat{BAC}}$
$\Rightarrow \frac{1}{sin\widehat{ACB}} = \frac{\sqrt{3}}{sin\widehat{ABC}} = \frac{2}{sin\widehat{BAC}}$
$\Rightarrow \frac{1}{sin\widehat{ACB}} = \frac{\sqrt{3}}{sin\widehat{60}} = \frac{2}{sin\widehat{BAC}} = 2$
$\Rightarrow sin\widehat{ACB} = \frac{1}{2}$ và $sin\widehat{BAC} = 1$
Như vậy $\widehat{ACB} = 30^{o}$ và $\widehat{BAC} = 90^{o}$
Bài tập 3.41. Cho tam giác ABC có c = 1, a = 2 và $\widehat{B} = 120^{o}$.
a) Tính b, $\widehat{A}$, $\widehat{C}$.
b) Tính diện tích của tam giác.
c) Tính độ dài đường cao kẻ từ B của tam giác.
Trả lời:
a) Áp dụng định lí côsin ta có:
$b^{2} = a^{2} + c^{2} - 2accosB = 2^{2} + 1^{2} - 2.2.1.cos120 = 7$
$\Rightarrow b = \sqrt{7}$
Tương tự ta có $a^{2} = b^{2} + c^{2} - 2bccosA$
$\Rightarrow cosA = \frac{b^{2}+c^{2}-a^{2}}{2bc} = \frac{(\sqrt{7})^{2}+1^{2}-2^{2}}{2.\sqrt{7}.1} = \frac{2\sqrt{7}}{7}$
$\Rightarrow A \approx 41^{o}$
$cosC = \frac{a^{2}+b^{2}-c^{2}}{2bab} = \frac{2^{2}+(\sqrt{7})^{2}-1^{2}}{2.2.\sqrt{7}} = \frac{5\sqrt{7}}{14}$
$\Rightarrow A \approx 19^{o}$
b) Áp dụng công thức tính diện tích tam giác ta có:
$S = \frac{1}{2}acsinB = \frac{1}{2}.2.1.sin120 = \frac{\sqrt{3}}{2}$
c) Áp dụng công thức tính diện tích tam giác ta có:
$S = \frac{1}{2}bh_{b}$
$\Rightarrow h_{b} = \frac{2S}{b} = \frac{2.\frac{\sqrt{3}}{2}}{\sqrt{7}} = \frac{\sqrt{21}}{7}$
Bài tập 3.42. Cho tam giác ABC có a = 3, b = 5 và c = 7.
a) Tính các góc của tam giác, làm tròn đến độ.
b) Tính bán kính đường tròn nội tiếp và đường tròn ngoại tiếp của tam giác.
Trả lời:
a) Áp dụng định lí côsin trong tam giác ta có:
$a^{2}=b^{2}+c^{2}-2bc.cosA$
$\Rightarrow 3^{2} = 5^{2}+7^{2}-2.5.7.cosA$
$\Rightarrow cosA = \frac{13}{14}$
$\Rightarrow \widehat{A} \approx 22^{o}$
$b^{2}=a^{2}+c^{2}-2ac.cosB$
$\Rightarrow 5^{2} = 3^{2}+7^{2}-2.3.7.cosA$
$\Rightarrow cosA = \frac{11}{14}$
$\Rightarrow \widehat{B} \approx 38^{o}$
$c^{2}=a^{2}+b^{2}-2ab.cosC$
$\Rightarrow 7^{2} = 3^{2}+5^{2}-2.3.5.cosA$
$\Rightarrow cosA = \frac{-1}{2}$
$\Rightarrow \widehat{C} = 120^{o}$
b) Nửa chu vi tam giác:
$p = \frac{a+b+c}{2} = \frac{3+5+7}{2} = \frac{15}{2}$
Diện tích tam giác:
S = $\sqrt{p(p-a)(p-b)(p-c)}$ = $\sqrt{\frac{15}{2}(\frac{15}{2}-3)(\frac{15}{2}-5)(\frac{15}{2}-7)}$ = $\frac{15\sqrt{3}}{4}$
Áp dụng công thức tính diện tích tam giác ta có:
S = p.r
$\Rightarrow r = \frac{S}{p} = \frac{\frac{15\sqrt{3}}{4}}{\frac{15}{2}} = \frac{\sqrt{3}}{2}$
Áp dụng công thức tính diện tích tam giác ta có:
$S = \frac{abc}{4R}$
$\Rightarrow R = \frac{abc}{4S} = \frac{3.5.7}{4.\frac{15\sqrt{3}}{4}} = \frac{7\sqrt{3}}{3}$
Bài tập 3.43. Cho tam giác ABC có $\widehat{B} = 45^{o}$ , $\widehat{C} = 15^{o}$ và b = $\sqrt{2}$. Tính a, $h_{a}$.
Trả lời:
$\frac{a}{sinA} = \frac{b}{sinB}$
$\Rightarrow a = \frac{b}{sinB}.sinA = \frac{\sqrt{2}}{sin45}.sin120 = \sqrt{3}$
Áp dụng công thức tính diện tích tam giác ta có:
$S = \frac{1}{2}ab.sinC = \frac{1}{2}.\sqrt{3}.\sqrt{2}.sin15 = \frac{3-\sqrt{3}}{4}$
$S = \frac{1}{2}a.h_{a}$
$\Rightarrow h_{a} = \frac{2S}{a} = \frac{2.\frac{3-\sqrt{3}}{4}}{\sqrt{3}} = \frac{-1+\sqrt{3}}{2}$
Bài tập 3.44. Cho tam giác ABC, có c = 5, a = 8 và $\widehat{B} = 60^{o}$.
a) Tính b và số đo các góc A, C (số đo các góc làm tròn đến hàng đơn vị, theo đơn vị độ).
b) Tính độ dài đường cao kẻ từ B.
c) Tính độ dài trung tuyến kẻ từ A.
Trả lời:
a) Áp dụng định lí côsin tam giác ta có:
$b^{2} = a^{2} + c^{2} -2ac.cosB = 8^{2} + 5^{2} - 2.8.5.cos60 = 49$
$\Rightarrow b = 7$
$a^{2} = b^{2} + c^{2} - 2bc.cosA$
$\Rightarrow cosA = \frac{b^{2}+c^{2}-a^{2}}{2bc} = \frac{7^{2}+5^{2}-8^{2}}{2.5.7} = \frac{1}{7}$
$\Rightarrow \widehat{A} \approx 82^{o}$
$c^{2} = a^{2} + b^{2} -2ab.cosC$
$\Rightarrow cosC = \frac{a^{2} + b^{2} - c^{2}}{2ab}$
$\Rightarrow \widehat{C} = 38^{o}$
b) Áp dụng tính diện tích tam giác ta có:
$S = \frac{1}{2}ac.sinB = \frac{1}{2}.8.5.sin60 = 10\sqrt{3}$
$S = \frac{1}{2}bh_{b}$
$h_{b} = \frac{2S}{b} = \frac{2.10\sqrt{3}}{7} = \frac{20\sqrt{3}}{7}$
c) Áp dụng công thức tính độ dài đường trung tuyến tam giác ta có:
$m_{a}^{2} = \frac{b^{2}+c^{2}}{2} - \frac{a^{2}}{4} = \frac{7^{2}+5^{2}}{2} - \frac{8^{2}}{4} = 21$
$\Rightarrow m_{a} = \sqrt{21}$
Bài tập 3.45. Cho tam giác ABC có $\widehat{B} = 15^{o}, \widehat{C} = 30^{o}$ và c = 2.
a) Tính số đo góc A và độ dài các cạnh a, b.
b) Tính diện tích và bán kính đường tròn ngoại tiếp của tam giác.
c) Lấy điểm D thuộc cạnh AB sao cho $\widehat{BCD} = \widehat{DCA}$ (tức CD là phân giác của góc $\widehat{BCA}$). Tính độ dài CD.
Trả lời:
a) Có $\widehat{A} = 180^{o} - \widehat{B} - \widehat{C} =180^{0} - 15^{o} -30^{o} = 135^{o}$
Áp dụng định lí sin ta có:
$\frac{a}{sinA} = \frac{b}{sinB} = \frac{c}{sinC}$
$\Rightarrow \frac{a}{sin135} = \frac{b}{sin15} = \frac{c}{sin30} = 4$
$\Rightarrow a = 4sin135 = 2\sqrt{2}, b = 4sin15 = \sqrt{6}-\sqrt{2}$
b) Áp dụng công thức tính diện tích tam giác ta có:
$S = \frac{1}{2}ac.sinB = \frac{1}{2}.2\sqrt{2}.(\sqrt{6}-\sqrt{2}).sin30= -1 + \sqrt{3}$
$\Rightarrow R = \frac{abc}{4S} = \frac{2\sqrt{2}.(\sqrt{6}-\sqrt{2}).2}{4.(-1+\sqrt{3})} = 2$
c)

CD là phân giác của góc $\widehat{BCA}$ nên $\widehat{BCD}$ = $\widehat{DCA}$ = $\frac{1}{2}\widehat{BCA} = \widehat{B} = 15^{o}$
Tam giác BCD là tam giác cân tại D
Giả sử I là trung điểm của BC
Khi đó DI là đường trung tuyến đồng thời là đường cao
$\Rightarrow IB = IC \frac{1}{2}BC = \frac{1}{2}.2\sqrt{2} = \sqrt{2}$
Xét tam giác CDI vuông tại I ta có:
$CD = \frac{CI}{cos\widehat{ICD}} = \frac{\sqrt{2}}{cos15} = -2 +2\sqrt{3}$
Bài tập 3.46. Trên biển, một tàu cá xuất phát từ cảng A, chạy về phương đông 15 km tới B, rồi chuyên sang hướng $E30^{o}S$ chạy tiếp 20 km nữa tới đảo C.
a) Tính khoảng cách từ A tới C (làm tròn đến hàng đơn vị, theo đơn vị kilômét).
b) Xác định hướng từ A tới C (làm tròn đến hàng đơn vị, theo đơn vị độ).
Trả lời:

a) Tàu cá xuất phát từ cảng A, chạy theo phương đông tới B, rồi chuyển sang hướng $E30^{o}S$, chạy tiếp tới đảo C nên ta có:
$\widehat{ABC} = 180^{o} - 30^{o} = 150^{o}$
Áp dụng định lí côsin ta có:
$AC^{2} = AB^{2} + BC^{2} -2.AB.BC.cos\widehat{ABC} = 15^{2} + 20^{2} -2.15.20.cos150 = 625 + 300\sqrt{3}$
$\Rightarrow AC \approx 34$ (km)
b) Áp dụng định lí sin ta có:
$\frac{BC}{sin\widehat{CAB}} = \frac{AC}{sin\widehat{ABC}}$
$\Rightarrow sin\widehat{CAB} = \frac{sin\widehat{ABC}}{AC}.BC = \frac{sin150}{34}.20 \approx 0,294$
$\Rightarrow \widehat{CAB} \approx 17^{o}$
Bài tập 3.47. Trên sườn đồi, với độ dốc 12% (độ dốc của sườn đồi được tính bằng tang của góc nhọn tạo bởi sườn đồi với phương nằm ngang) có một cây cao mọc thẳng đứng. Ở phía chân dôdi, cách gốc cây 30 m, người ta nhìn ngọn cây dưới một góc $45^{o}$ so với phương nằm ngang. Tính chiều cao của cây đó (làm tròn đến hàng đơn vị, theo đơn vị mét).
Trả lời:

Sườn đồi có độ dốc 12% (độ dốc của sườn đồi được tính bằng tang của góc nhọn tạo bởi sườn đồi với phương nằm ngang) nên $tan\widehat{HAB} = 12% = 0,12$
$\Rightarrow \widehat{HAB} \approx 7^{o}$
Cho nên $\widehat{BAC} = \widehat{HAC} - \widehat{HAB} = 45^{o} - 7^{o} = 38^{o}$
$\widehat{BCA} = 90^{o} - \widehat{HAC} = 90^{o} - 45^{o} = 45^{o}$
Áp dụng định lí sin ta có:
$\frac{BC}{sin\widehat{BAC}} = \frac{AB}{sin\widehat{BCA}}$
$\Rightarrow BC = \frac{AB}{sin\widehat{BCA}} . sin\widehat{BAC} = \frac{30}{sin45} . sin38 \approx 26$ (m)
Ngoài giải bài tập Toán lớp 10 Kết Nối Tri Thức của Giaibaitapsgk sẽ cung cấp đầy đủ từng bước trong bài giải vở bài tập Toán lớp 10. Dựa vào đó các em cũng có thể nhận ra những điểm sai hoặc thiếu của mình khi làm bài và chủ động sửa đổi.
Toàn bộ hướng dẫn giải bài tập Toán lớp 10 sách Kết Nối Tri Thức sẽ là tài liệu hữu ích giúp các em học sinh rút ngắn thời gian làm bài tập về nhà, bậc phụ huynh có thể hiểu được cách giải Toán 10theo chương trình mới. Song song với đó Giaibaitapsgk cũng cung cấp bộ câu hỏi trắc nghiệm, phiếu bài tập cuối tuần để thầy cô, phụ huynh tham khảo giúp con có thêm cơ hội rèn luyện với nhiều dạng Toán lớp 10 nâng cao khác nhau.
