Giải SBT toán 10 kết nối Bài tập cuối chương II
Tài liệu hướng dẫn giải Toán lớp 10 Kết Nối Tri Thức của Giaibaitapsgk có đủ cả tập 1, tập 2 và được chia theo từng tuần học đảm bảo các em có thể nhanh chóng tra cứu. Dựa vào đáp án để so sánh kết quả nhận ra điểm sai trong các bước giải của mình, đồng thời cũng làm quen với các dạng toán quan trọng trong chương trình Toán lớp 10. Ngoài ra, chúng tôi cũng hỗ trợ giải vở bài tập Toán 10 theo từng trang.
Hướng dẫn giải Bài tập cuối chương 2 trang 24 SBT toán 10 tập 1. Đây là sách bài tập nằm trong bộ sách "Kết nối tri thức" được biên soạn theo chương trình đổi mới của Bộ giáo dục. Hi vọng, với cách hướng dẫn cụ thể và giải chi tiết học sinh sẽ nắm bài học tốt hơn.
Bài tập 2.10. Trong các bất phương trình sau, bất phương nào là bất phương trình bậc nhất hai ẩn?
A. 2$x^{2}$ + 3y > 4. B. xy + y < 5.
C. 3$x^{2}$ + $4^{3}$y $\geq$ 6. D. x + $y^{3}$ $\leq$ 3.
Trả lời: Chọn đáp án: C. 3$x^{2}$ + $4^{3}$y $\geq$ 6.
Bài tập 2.11. Trong các hệ bất phương trình sau, hệ bất phương trình nào hệ bất phương trình bậc nhất hai ẩn?
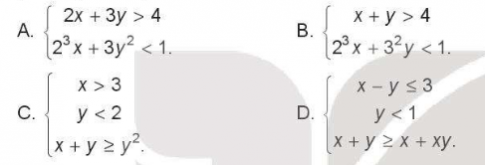
Trả lời: Chọn đáp án: 
Bài tập 2.12. Điểm nào dưới đây thuộc miền nghiệm của bất phương trình 2x + 5y $\leq$ 10?
A. (5; 2). B. (-1; 4).
C. (2; 1). D. (-5; 6).
Trả lời: Chọn đáp án: C. (2; 1).
Thay x = 4; y = 2 vào 2x + 5y ta được 2 . 4 + 5. 2 = 18 > 10
Thay x = -1; y = 4 vào 2x + 5y ta được 2 . (-1) + 5 . 4 = 18 > 10
Thay x = -5; y = 6 vào 2x + 5y ta được 2 . (-5) + 5 . 6 = 20 > 10
Thay x = 2; y = 1 vào 2x + 5y ta được 2 . 2 + 5 . 1 = 9 < 10
Bài tập 2.13. Điểm nào dưới đây không thuộc miền nghiệm của bất phương trình 2x - 3y > 13?
A. (1; -5). B. (-1; 4).
C. (3; -3). D. (8; 1).
Trả lời: Chọn đáp án: D. (8; 1).
Thay x = 1; y = -5 vào 2x - 3y ta được 2 . 1 - 3 . (-5) = 17 > 13
Thay x = 2; y = -4 vào 2x - 3y ta được 2 . 2 - 3 . (-4) = 16 > 13
Thay x = 3; y = -3 vào 2x - 3y ta được 2 . 3 - 3 . (-3) = 15 > 13
Thay x = 8; y = 1 vào 2x - 3y ta được 2 . 8 - 3 . 1 = 13
Bài tập 2.14. Cho bắt phương trình x + 2y < 3. Khẳng định nào sau đây là đúng?
A. Miền nghiệm của bất phương trình là nửa mặt phẳng bờ d: x + 2y = 3 chứa gốc toạ độ.
B. Miền nghiệm của bất phương trình là nửa mặt phẳng bờ d: + 2y = 3 không chứa gốc toạ độ.
C. Miền nghiệm của bất phương trình là nửa mặt phẳng bờ d: x + 2y = -3 chứa gốc toạ độ.
D. Miền nghiệm của bắt phương trình là nửa mặt phẳng bờ d: x + 2y = -3 không chứa gốc toạ độ.
Trả lời: Chọn đáp án: A. Miền nghiệm của bất phương trình là nửa mặt phẳng bờ d: x + 2y = 3 chứa gốc toạ độ.
Bài tập 2.15. Cặp số nào dưới đây là nghiệm của bất phương trình 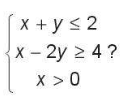
A. (-1; 2). B. (-2; -4).
C. (0; 1). D. (2; -4).
Trả lời: Chọn đáp án: D. (2; -4).
Bài tập 2.16. Điểm nào dưới đây thuộc miền nghiệm của hệ bất phương trình 
A. (-3; 2). B. (0; 1).
C. (4; -1). D. (-2; 2).
Trả lời: Chọn đáp án: C. (4; -1).
Bài tập 2.17. Miền nghiệm của hệ bất phương trình nào dưới đây là miền tam giác ABC (miền không bị gạch)?
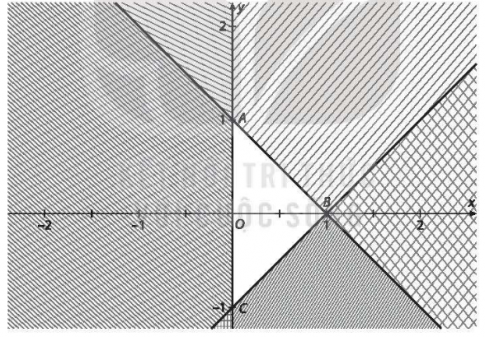

Trả lời: Chọn đáp án: 
Bài tập 2.18. Miền nghiệm của hệ bất phương trình 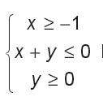 là
là
A. Một nửa mặt phẳng. B. Miền tam giác.
C. Miền tứ giác. D. Miền ngũ giác.
Trả lời: Chọn đáp án: B. Miền tam giác.

Bài tập 2.19. Miền nghiệm của hệ bất phương trình 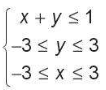 là
là
A. Miền lục giác. B. Miền tam giác.
C. Miền tứ giác. D. Miền ngũ giác.
Trả lời: Chọn đáp án: D. Miền ngũ giác.

Bài tập 2.20. Miền nghiệm của hệ bất phương trình 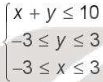 là
là
A. Miền lục giác. B. Miền tam giác.
C. Miền tứ giác. D. Miền ngũ giác.
Trả lời: Chọn đáp án: C. Miền tứ giác.

Bài tập 2.21. Giá trị lớn nhấ của biểu thức F(x; y) = 3x + y với (x; y) thuộc miền nghiệm của hệ bất phương trình 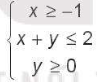 là
là
A. -3. B. 6. C. 5. D. 8.
Trả lời: Chọn đáp án: B. 6.
Đường thẳng d1: x = -1 là đường thẳng song song với trục Oy và đi qua điểm có hoành độ bằng -1.
Chọn điểm I(0; 1) $\notin$ d1 và thay vào biểu thức x được 0 > -1
Suy ra miền nghiệm của bất phương trình x $\geq$ -1 là nửa mặt phẳng bờ d1 chứa điểm I(0; 1)
Vẽ đường thẳng d2: x + y = 2 bằng cách vẽ một đường thẳng đi qua hai điểm (0; 2) và (2; 0)
Chọn điểm I(0; 1) $\notin$ d2 và thay vào biểu thức x + y được 1 < 2
Suy ra miền nghiệm của bất phương trình x + y $\leq$ 2 là nửa mặt phẳng bờ d2 chứa điểm I(0; 1)
Đường thẳng d3: y = 0 là đường thẳng trùng với trục Ox
Chọn điểm I(0; 1) $\notin$ d3 và thay vào biểu thức y được 1 > 0
Suy ra miền nghiệm của bất phương trình y $\geq$ 0 là nửa mặt phẳng bờ d3 chứa điểm I(0; 1)
Như vậy, miền nghiệm của hệ bất phương trình là miền tam giác với các đỉnh (-1; 3), (-1; 0) và (2; 0)
Ta có F(-1; 3) = 3 . (-1) + 3 = 0
F(-1; 0) = 3 . (-1) + 0 = -3
F(2; 0) = 3 . 2 + 0 = 6
Bài tập 2.22. Giá trị nhỏ nhất của biểu thức F(x; y) = -x + 4y với (x; y) thuộc miền nghiệm của hệ bất phương trình 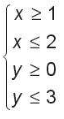 là
là
A. -2. B. 3. C. 11. D. -4.
Trả lời: Chọn đáp án: A. -2.
Đường thẳng d1: x = 1 là đường thẳng song song với trục Oy và đi qua điểm có hoành độ bằng 1
Chọn điểm I(1,5; 1) $\notin$ d1 và thay vào ta được 1,5 > 1
Suy ra miền nghiệm của bất phương trình x $\geq$ 1 là nửa mặt phẳng bờ d1 có chứa điểm I(1,5; 1)
Đường thẳng d2: x = 2 là đường thẳng song song với trục Oy và đi qua điểm có hoành độ bằng 2
Chọn điểm I(1,5; 1) $\notin$ d2 và thay vào ta được 1,5 < 2
Suy ra miền nghiệm của bất phương trình x $\leq$ 2 là nửa mặt phẳng bờ d2 có chứa điểm I(1,5; 1)
Đường thẳng d3: y = 0 là đường thẳng trùng với trục Ox
Chọn điểm I(1,5; 1) $\notin$ d3 và thay vào ta được 1 > 0
Suy ra miền nghiệm của bất phương trình y $\geq$ 0 là nửa mặt phẳng bờ d3 có chứa điểm I(1,5; 1)
Đường thẳng d4: y = 3 là đường thẳng song song với trục Ox và đi qua điểm có tung độ bằng 3
Chọn điểm I(1,5; 1) $\notin$ d3 và thay vào biểu thức y ta được 1 < 3
Suy ra miền nghiệm của bất phương trình y $\leq$ 3 là nửa mặt phẳng bờ d4 có chứa điểm I(1,5; 1)
Như vậy, miền nghiệm của hệ bất phương trình trên là miền tứ giác với các đỉnh (1; 0), (1; 3), (2; 3) và (2; 0)
F(1; 0) = -1 + 4 . 0 = -1
F(1; 3) = -1 + 4 . 3 = 11
F(2; 3) = -2 + 4 . 3 = 10
F(2; 0) = -2 + 4 . 0 = -2
Bài tập 2.23. Tổng của giá trị lớn nhất và giá trị nhỏ nhất của biểu thức F(x; y) = x + 5y với (x; y) thuộc miền nghiệm của hệ bất phương trình 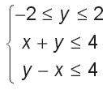 là:
là:
A. -20. B. -4. C. 28. D. 16.
Trả lời: Chọn đáp án: B. -4.
Đường thẳng d1: y = -2 là đường thẳng song song với trục Ox và đi qua điểm có tung độ bằng -2.
Chọn điểm O(0; 0) $\notin$ d1 và thay được 0 > -2.
Suy ra miền nghiệm của bất phương trình -2 $\leq$ y là nửa mặt phẳng bờ d1 chứa điểm O(0; 0).
Đường thẳng d2: y = 2 là đường thẳng song song với trục Ox và đi qua điểm có tung độ bằng 2.
Chọn điểm O(0; 0) $\notin$ d2 và thay vào được 0 < 2.
Suy ra miền nghiệm của bất phương trình y $\leq$ 2 là nửa mặt phẳng bờ d2 chứa điểm O(0; 0)
Vẽ đường thẳng d3: x + y = 4 bằng cách vẽ đường thẳng đi qua hai điểm (0; 4) và (4; 0)
Chọn điểm O(0; 0) $\notin$ d3 và thay vào được 0 < 4
Suy ra miền nghiệm của bất phương trình x + y $\leq$ 4 là nửa mặt phẳng bờ d3 chứa điểm O(0; 0)
Vẽ đường thẳng d4: y - x = 4 bằng cách vẽ đường thẳng đi qua hai điểm (0; 4) và (1; 5)
Chọn điểm O(0; 0) $\notin$ d4 và thay vào được 0 < 4
Suy ra miền nghiệm của bất phương trình y - x $\leq$ 4 là nửa mặt phẳng bờ d4 chứa điểm O(0; 0)
Như vậy, miền nghiệm của hệ bất phương trình trên là miền tứ giác với các đỉnh (-6; -2), (-2; 2), (2;2) và (6; -2)
F(-6; -2) = -6 + 5 . (-2) = -16;
F(-2; 2) = -2 + 5 . 2 = 8;
F(2; 2) = 2 + 5 . 2 = 12;
F(6; -2) = 6 + 5 . (-2) = -4.
Do đó giá trị lớn nhất của F(x; y) = 12 và giá trị nhỏ nhất của F(x; y) = -16.
Bài tập 2.24. Một hợp tác xã chăn nuôi dự định trộn hai loại thức ăn gia súc X và Y để tạo thành thức ăn hỗn hợp cho gia súc. Giá một bao loại X là 250 nghìn đồng, giá một bao loại Y là 200 nghìn đồng. Mỗi bao loại X chứa 2 đơn vị chất dinh dưỡng A, 2 đơn vị chất dinh dưỡng B và 2 đơn vị chất dinh dưỡng C. Mỗi bao loại Y chứa 1 đơn vị chất dinh dưỡng A, 9 đơn vị chất dinh dưỡng B và 3 đơn vị chất dinh dưỡng C. Tìm chi phí nhỏ nhất để mua hai loại thức ăn gia súc X và Y sao cho hỗn hợp thu được chứa tối thiểu 12 đơn vị chất dinh dưỡng A, 36 đơn vị chất dinh đưỡng B và 24 đơn vị chất dinh dưỡng C.
A. 1,95 triệu đồng. B. 4,5 triệu đồng.
C. 1,85 triệu đồng. D. 1,7 triệu đồng.
Trả lời:
Gọi số bao loại X và số bao loại Y lần lượt là x bao và y bao (x, y $\in$ ℕ).
Mỗi bao loại X chứa 2 đơn vị chất dinh dưỡng A, 2 đơn vị chất dinh dưỡng B và 2 đơn vị chất dinh dưỡng C nên x bao loại X chứa 2x đơn vị chất dinh dưỡng A, 2x đơn vị chất dinh dưỡng B và 2x đơn vị chất dinh dưỡng C.
Mỗi bao loại Y chứa 1 đơn vị chất dinh dưỡng A, 9 đơn vị chất dinh dưỡng B và 3 đơn vị chất dinh dưỡng C nên y bao loại Y chứa y đơn vị chất dinh dưỡng A, 9y đơn vị chất dinh dưỡng B và 3y đơn vị chất dinh dưỡng C.
Hỗn hợp thu được chứa tối thiểu 12 đơn vị chất dinh dưỡng A, 36 đơn vị chất dinh dưỡng B và 24 đơn vị chất dinh dưỡng C nên ta có các phương trình:
2x + y ≥ 12; 2x + 9y ≥ 36; 2x + 3y ≥ 24.
Khi đó ta có hệ bất phương trình sau 

Chi phí để mua hai loại thức ăn là F(x; y) = 250x + 200y (nghìn đồng).
Thay giá trị tại các đỉnh ta có F(0; 12) = 2 400, F(3; 6) = 1 950, F(9; 2) = 2 650, F(18; 0) = 4 500. Do đó, giá trị nhỏ nhất là F(3; 6) = 1 950. Vậy chi phí nhỏ nhất để mua hai loại thức ăn là 1,95 triệu đồng.
Bài tập 2.25. Biểu diễn miền nghiệm của bất phương trình bậc nhất hai ẩn sau trên mặt phẳng tọa độ:
a) x + y $\geq$ -4; b) 2x - y $\leq$ 5;
c) x + 2y < 0; d) -x + 2y >0.
Trả lời:
a) Vẽ đường thẳng d1: x + y = -4 bằng cách vẽ đường thẳng đi qua hai điểm (0; -4) và (-4; 0)
Chọn điểm O(0; 0) $\notin$ d1 và thay vào biểu thức x + y ta được 0 > -4
Suy ra miền nghiệm của bất phương trình x + y $\geq$ -4 là nửa mặt phẳng bờ d1 chứa điểm O(0; 0)
b) Vẽ đường thẳng d1: 2x - y = 5 bằng cách vẽ đường thẳng đi qua hai điểm (0; -5) và (3; 1)
Chọn điểm O(0; 0) $\notin$ d1 và thay vào biểu thức 2x - y ta được 0 < 5
Suy ra miền nghiệm của bất phương trình 2x - y $\geq$ 5 là nửa mặt phẳng bờ d1 chứa điểm O(0; 0)
c) Vẽ đường thẳng d1: x + 2y = 0 bằng cách vẽ đường thẳng đi qua hai điểm (0; 0) và (2; -1)
Chọn điểm I(1; 1) $\notin$ d1 và thay vào biểu thức x + 2y ta được 1 + 2 . 1 = 3 > 0
Suy ra miền nghiệm của bất phương trình x + 2y < 0 là nửa mặt phẳng bờ d1 không chứa điểm I(1; 1) và bỏ đi đường thẳng d1
d) Vẽ đường thẳng d1: -x + 2y = 0 bằng cách vẽ đường thẳng đi qua hai điểm (0; 0) và (2; 1)
Chọn điểm I(1; 1) $\notin$ d1 và thay vào biểu thức -x + 2y ta được 1 > 0
Suy ra miền nghiệm của bất phương trình -x + 2y > 0 là nửa mặt phẳng bờ d1 chứa điểm I(1; 1) và bỏ đi đường thẳng d1
Bài tập 2.26. Biểu diễn miền nghiệm của các hệ bất phương trình bậc nhất hai ẩn sau trên mặt phẳng tọa độ:
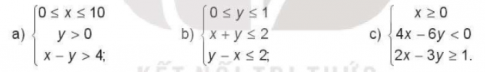
Trả lời:
a) Đường thẳng d1: x = 0 là đường thẳng trùng với trục Oy
Chọn điểm I(1; 1) $\notin$ d1 và thay vào x ta được 1 > 0
Miền nghiệm của bất phương trình x $\geq$ 0 là nửa mặt phẳng bờ d1 chứa điểm I(1; 1)
Đường thẳng d2: x = 10 là đường thẳng song song với trục Oy và đi qua điểm có hoành độ bằng 10
Miền nghiệm của bất phương trình x $\leq$ 10 là nửa mặt phẳng bờ d2 chứa điểm I(1; 1)
Đường thẳng d3: y = 0 là đường thẳng trùng với trục Ox
Chọn điểm I(1; 1) $\notin$ d3 và thay vào y ta được 1 > 0
Miền nghiệm của bất phương trình y > 0 là nửa mặt phẳng bờ d3 chứa điểm I(1; 1) và bỏ đi đường thẳng d3
Vẽ đường thẳng d4: x - y = 4 bằng cách vẽ đường thẳng đi qua hai điểm (4; 0) và (0; -4)
Chọn điểm I(1; 1) $\notin$ d4 và thay vào x - y ta được 0 < 4
Miền nghiệm của bất phương trình x - y > 4 là nửa mặt phẳng bờ d4 không chứa điểm I(1; 1) và bỏ đi đường thẳng d4
b) Đường thẳng d1: y = 0 là đường thẳng trùng với trục Ox
Chọn điểm I(0; 0,5) $\notin$ d1 và thay vào y ta được 0,5 > 0
Miền nghiệm của bất phương trình y $\geq$ 0 là nửa mặt phẳng bờ d1 chứa điểm I(0; 0; 5)
Đường thẳng d2: y = 1 là đường thẳng song song với trục Ox và đi qua điểm có tung độ bằng 1
Chọn điểm I(0; 0,5) $\notin$ d2 và thay vào y ta được 0,5 < 1
Miền nghiệm của bất phương trình y $\leq$ 1 là nửa mặt phẳng bờ d2 chứa điểm I(0; 0; 5)
Vẽ đường thẳng d3: x + y = 2 bằng cách vẽ đường thẳng đi qua hai điểm (2; 0) và (0; 2)
Chọn điểm I(0; 0,5) $\notin$ d3 và thay vào biểu thức x + y ta được 0,5 < 2
Miền nghiệm của bất phương trình x + y $\leq$ 2 là nửa mặt phẳng bờ d3 chứa điểm I(0; 0; 5)
Vẽ đường thẳng d4: y - x = 2 bằng cách vẽ đường thẳng đi qua hai điểm (0; 2) và (-2; 0)
Chọn điểm I(0; 0,5) $\notin$ d4 và thay vào y - x ta được 0,5 < 2
Miền nghiệm của bất phương trình y - x $\leq$ 2 là nửa mặt phẳng bờ d4 chứa điểm I(0; 0; 5)
c) Đường thẳng d1: x = 0 là đường thẳng trùng với trục Oy
Chọn điểm I(1; 1) $\notin$ d1 và thay vào biểu thức x ta được 1 > 0
Miền nghiệm của bất phương trình x $\geq$ 0 là nửa mặt phẳng bờ d1 chứa điểm I(1; 1)
Vẽ đường thẳng d2: 4x - 6y = 0 bằng cách vẽ đường thẳng đi qua hai điểm (0; 0) và (3; 2)
Chọn điểm I(1; 1) $\notin$ d2 và thay vào 4x - 6y ta được -2 < 0
Miền nghiệm của bất phương trình 4x - 6y < 0 là nửa mặt phẳng bờ d2 chứa điểm I(1; 1) và bỏ đi đường thẳng d2
Vẽ đường thẳng d3: 2x - 3y = 1 bằng cách vẽ đường thẳng đi qua hai điểm (2; 1) và (5; 3)
Chọn điểm I(1; 1) $\notin$ d3 và thay vào 2x - 3y ta được -1 < 1
Miền nghiệm của bất phương trình 2x - 3y $\geq$ 1 là nửa mặt phẳng bờ d3 không chứa điểm I(1; 1)
Bài tập 2.27. Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức F(x; y) = 2x + 3y với (x;y) thuộc miền nghiệm của hệ bất phương trình 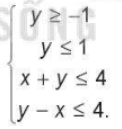
Trả lời:
Đường thẳng $d_{1}$: y = -1 là đường thẳng song song với trục Ox đi qua điểm có tung độ bằng -1
Chọn điểm O(0; 0) $\notin$ $d_{1}$ và thay vào y ta được 0 > -1
Miền nghiệm của bất phương trình y $\geq$ -1 là nửa mặt phẳng bờ $d_{1}$ chứa điểm O(0; 0)
Đường thẳng $d_{2}$: y = 1 là đường thẳng song song với trục Ox đi qua điểm có tung độ bằng 1
Chọn điểm O(0; 0) $\notin$ $d_{2}$ và thay vào y ta được 0 < 1
Miền nghiệm của bất phương trình y $\leq$ 1 là nửa mặt phẳng bờ $d_{2}$ chứa điểm O(0; 0)
Vẽ đường thẳng $d_{3}$: x + y = 4 bằng cách vẽ đường thẳng đi qua hai điểm (0; 4) và (4; 0)
Chọn điểm O(0; 0) $\notin$ $d_{3}$ và thay vào biểu thức x + y ta được 0 < 4
Suy ra miền nghiệm của bất phương trình x + y $\leq$ 4 là nửa mặt phẳng bờ $d_{3}$ chứa điểm O(0; 0)
Vẽ đường thẳng $d_{4}$: y - x = 4 bằng cách vẽ đường thẳng đi qua hai điểm (0; 4) và (-4; 0)
Chọn điểm O(0; 0) $\notin$ $d_{1}$ và thay vào biểu thức y - x ta được 0 < 4
Miền nghiệm của bất phương trình y - x $\leq$ 4 là nửa mặt phẳng bờ $d_{1}$ chứa điểm O(0; 0)
Miền nghiệm của hệ bắt phương trinh đã cho là hình thang ABCD với A(-5; -1), B(5; -1), C(3; 1) và D(-3; 1).
Tính giá trị của F tại các đỉnh ta được:
F(-5; -1) = 2 . (-5) + 3 . (-1) = -13
F(-3; 1) = 2 . (-3) + 3 . 1 = -3
F(3; 1) = 2 . 3 + 3 . 1 = 9
F(5; -1) = 2 . 5 + 3 . (-1) = 7
Khi đó giá trị nhỏ nhất của F(x; y) là F(-5; -1) = -13 và giá trị lớn nhất là F(3; 1) = 9.
Bài tập 2.28. Một phân xưởng có hai máy chuyên dụng $M_{1}$ và $M_{2}$ để sản xuất hai loại sản phẩm A và B theo đơn đặt hàng. Nếu sản xuất được một tấn sản phẩm loại A thì phân xưởng nhận được số tiền lãi là 2 triệu đồng. Nếu sản xuất được một tấn sản phẩm loại B thì phân xưởng nhận được số tiền lãi là 1.6 triệu đồng. Muốn sản xuất một tấn sản phẩm loại A, người ta phải dùng máy $M_{1}$ trong 3 giờ và máy $M_{2}$ trong 1 giờ. Muốn sản xuất một tấn sản phẩm loại B người ta phải dùng máy $M_{1}$ trong 1 giờ và máy $M_{2}$ trong 1 giờ. Một máy không thể dùng để sản xuất đồng thời hai loại sản phẩm. Máy M, làm việc không quá 6 giờ một ngàyvà máy $M_{1}$ làm việc không quá 4 giờ một ngày. Hỏi số tiền lãi lớn nhất mà phân xưởng này có thể thu được trong một ngày là bao nhiêu?
Trả lời:
Gọi số sản phẩm loại A và loại B sản xuất ra lần lượt là x tấn và y tấn (x, y $\geq$ 0)
Để sản xuất x tấn sản phẩm loại A thì máy $M_{1}$ cần hoạt động trong 3x giờ, máy $M_{2}$ cần hoạt động trong x giờ
Để sản xuất y tấn sản phẩm loại B thì máy $M_{1}$ cần hoạt động y giờ, máy $M_{2}$ cần hoạt động trong y giờ
Do máy $M_{1}$ làm việc không quá 6 giờ một ngày và máy $M_{2}$ làm việc không quá 4 giờ một ngày nên 3x + y $\leq$ 6; x + y $\leq$ 4
Khi đó ta có hệ phương trình 
F(x; y) = 2x + 1,6y (triệu đồng)
Miền nghiệm của hệ là miền tứ giác OABC với O(0. 0), A(0; 4), B(1; 3) và C(2; 0), ta có:
F(0; 0) = 2 . 0 + 1,6 . 0 = 0
F(0; 4) = 2 . 0 + 1,6 . 4 = 6,4
F(1; 3) = 2 . 1 + 1,6 . 3 = 6,8
F(2; 0) = 2 . 2 + 1,6 . 0 = 4
Khi đó giá trị của F(x; y) lớn nhất bằng 6,8
Bài tập 2.29. Giả sử một người ăn kiêng cần được cụng cấp ít nhất 300 calo, 36 đơn vị vitamin A và 90 đơn vị vitamin C mỗi ngày từ hai loại đồ uống I và II.
Mỗi cốc đồ uống I cung cấp 60 calo, 12 đơn vị vitamin A và 10 đơn vị vitamin C. Mỗi cốc đồ uống II cung cấp 60 calo, 6 đơn vị vitamin A và 30 đơn vị vitamin C. Biết rằng một cốc đồ uống I có giá 12 nghìn đồng và một cốc đồ uống II có giá 15 nghìn đồng.
a) Gọi x và y tương ứng là số cốc đô uống I và II. Viết các bất phương trình biểu thị các điều kiện của bài toán thành một hệ bất phương trình và xác định miền nghiệm của hệ đó.
b) Gọi F (nghìn đồng) là số tiền phải trà cho x cốc đồ uống I và y cốc đồ uống II. Hãy biểu diễn F theo x và y.
c) Biết rằng F đạt giá trị nhỏ nhất trên miền nghiệm tìm được ở câu a tại một trong các đỉnh của miền nghiệm, tìm giá trị nhỏ nhất đó. Từ đó suy ra người đó cần uống bao nhiêu cốc loại I và loại II để chi phí là nhỏ nhất mà vẫn đáp ứng được yêu cầu hằng ngày.
Trả lời:
a) Gọi x và y lần lượt là số cốc đồ uống I và II thoả mãn điều kiện đề bài.
Khi đó ta có x $\geq$ 0 và y $\geq$ 0. Hơn nữa, để người ăn kiêng được cung cấp đủ lượng calo và vitamin thì 60x + 60y $\geq$ 300, 12x + 6y $\geq$ 36 và 10x + 30y $\geq$ 90.
Từ đó, ta có hệ bất phương trình bậc nhất hai ẩn:

Miền nghiệm là miền không bị gạch với các đỉnh A(0; 6), B(1; 4), C(3; 2), D(9; 0) như hình dưới đây:

b) Chi phí cho hai loại đồ uống là F(x; y) = 12x + 15y (nghìn đồng).
c) Ta tính giá trị của F tại các đỉnh: F(0; 6) = 90, F(1; 4) = 72, F(3: 2) = 66, F(9; 0) = 108. Do đó F nhỏ nhất tại (x; y) = (3; 2).
Vậy người đó cần uống 3 cốc đồ uống I và 2 cốc đồ uống II để đạt được các mục tiêu đề ra.
Ngoài giải bài tập Toán lớp 10 Kết Nối Tri Thức của Giaibaitapsgk sẽ cung cấp đầy đủ từng bước trong bài giải vở bài tập Toán lớp 10. Dựa vào đó các em cũng có thể nhận ra những điểm sai hoặc thiếu của mình khi làm bài và chủ động sửa đổi.
Toàn bộ hướng dẫn giải bài tập Toán lớp 10 sách Kết Nối Tri Thức sẽ là tài liệu hữu ích giúp các em học sinh rút ngắn thời gian làm bài tập về nhà, bậc phụ huynh có thể hiểu được cách giải Toán 10theo chương trình mới. Song song với đó Giaibaitapsgk cũng cung cấp bộ câu hỏi trắc nghiệm, phiếu bài tập cuối tuần để thầy cô, phụ huynh tham khảo giúp con có thêm cơ hội rèn luyện với nhiều dạng Toán lớp 10 nâng cao khác nhau.
