Giải SBT toán 10 kết nối bài 3 Bất phương trình bậc nhất hai ẩn
Tài liệu hướng dẫn giải Toán lớp 10 Kết Nối Tri Thức của Giaibaitapsgk có đủ cả tập 1, tập 2 và được chia theo từng tuần học đảm bảo các em có thể nhanh chóng tra cứu. Dựa vào đáp án để so sánh kết quả nhận ra điểm sai trong các bước giải của mình, đồng thời cũng làm quen với các dạng toán quan trọng trong chương trình Toán lớp 10. Ngoài ra, chúng tôi cũng hỗ trợ giải vở bài tập Toán 10 theo từng trang.
Hướng dẫn giải bài 3 Bất phương trình bậc nhất hai ẩn trang 16 SBT toán 10 tập 1. Đây là sách bài tập nằm trong bộ sách "Kết nối tri thức" được biên soạn theo chương trình đổi mới của Bộ giáo dục. Hi vọng, với cách hướng dẫn cụ thể và giải chi tiết học sinh sẽ nắm bài học tốt hơn.
Bài tập 2.1. Cho bất phương trình bậc nhất hai ẩn -3x + y < 4.
a) Biểu diễn miền nghiệm của bất phương trình đã cho trên mặt phẳng toạ độ.
b) Từ đó suy ra miền nghiệm của bất phương trỉnh -3x + y < 4 và miền nghiệm của bất phương trình -3x + y > 4.
Trả lời:
a) Phương trình -3x + y = 4 có:
x | 0 | 1 |
y | 4 | 7 |
Đồ thị của đường thẳng d: -3x + y = 4 đi qua các điểm có tọa độ (0; 4) và (1; 7)
Miền nghiệm của bất phương trình -3x + y < 4 là nửa mặt phẳng bờ d chứa gốc tọa độ và bỏ đi đường thẳng d (miền không được gạch).

b) Miền nghiệm của bất phương trình -3x + y $\leq$ 4 là nửa mặt phẳng bờ d chứa gốc tọa độ (miền không được gạch).
Miền nghiệm của bất phương trình -3x + y $\geq$ 4 là nửa mặt phẳng bờ d không chứa gốc tọa độ (miền được gạch).

Bài tập 2.2. Cho bất phương trình 2x + 3y + 3 < 5x + 2y + 3.
Bằng cách chuyển vế, hãy đưa bất phương trình trên về dạng tổng quát của bất phương trình bậc nhất hai ẩn. Biểu diễn miền nghiệm của bất phương bậc nhất hai ắn đó trên mặt phẳng toạ độ.
Trả lời:
2x + 3y + 3 < 5x + 2y + 3
$\Rightarrow$ 2x + 3y + 3 - 5x - 2y - 3 $\leq$ 0
$\Rightarrow$ -3x + y $\leq$ 0
Xác định hai điểm thuộc đường thẳng d: -3x + y = 0
x | 0 | 1 |
y | 0 | 3 |
Đường thẳng d: -3x + y = 0 đi qua hai điểm có tọa độ (0; 0) và (1; 3)

Bài tập 2.3. Xác định một bất phương trình bậc nhất hai ẩn nhận nửa mặt phẳng bờ là đường thăng d (miễn không bị gạch) làm miền nghiệm (H.2.3).
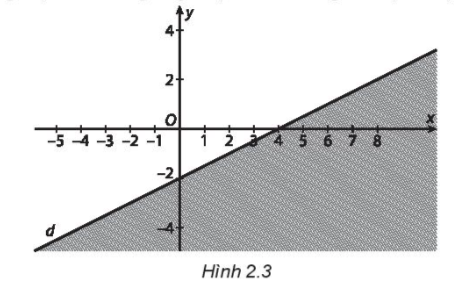
Trả lời:
Đường thẳng d đi qua hai điểm (0; -2) và (4; 0).
Gọi phương trình đường thẳng d: y = ax b (a ≠ 0).
Thay x = 0; y = -2 vào đường thẳng d ta có: -2 = a . 0 + b $\Rightarrow$ b = -2.
Thay x = 4; y = 0 vào đường thẳng d ta có: 0 = 4 . a + (-2) $\Rightarrow$ 2 = 4 . a $\Rightarrow$ a = $\frac{2}{4}$ = $\frac{1}{2}$
Do đó phương trình đường thẳng d: y = $\frac{1}{2}$x - 2 $\Rightarrow $2y = x - 4 $\Rightarrow$x - 2y = 4.
Chọn điểm O(0; 0) là điểm không thuộc đường thẳng d và thay vào biểu thức x - 2y ta được: 0 - 2 . 0 = 0 < 4.
Do đó bất phương trình nhận nửa mặt phẳng bờ là đường thẳng d (miền không bị gạch) làm miền nghiệm là x - 2y ≤ 4.
Bài tập 2.4. Cho bất phương trinh x + 2y $\geq$ -4.
a) Biểu diễn miền nghiệm của bất phương trình đã cho trên mặt phẳng toạ độ.
b) Miền nghiệm có chứa bao nhiêu điểm (x; y) với x, y là các số nguyên âm?
Trả lời:
a) Xác định hai điểm thuộc đường thẳng d: x + 2y = -4:
Có bảng sau:
x | 0 | -4 |
y | -2 | 0 |
Do đó đường thẳng d: x + 2y = -4 đi qua hai điểm (0; -2) và (-4; 0).
Chọn điểm O(0; 0) không thuộc đường thẳng d và thay vào biểu thức x + 2y ta được 0 + 2 . 0 = 0 > -4.
Do đó miền nghiệm của bất phương trình x + 2y $\geq$ -4 là nửa mặt phẳng bờ d chứa gốc tọa độ (miền không được gạch).

b) Do x, y là các số nguyên âm và x + 2y $\geq$ -4 nên 0 > x > -4.
Với y $\leq$ -2 thì 2y $\leq$ -4, mà x là số nguyên âm nên x + 2y < -4 (loại).
Do đó 0 > y > -2 suy ra y = -1.
Có bảng sau:
x | -1 | -2 | -3 |
y | -1 | -1 | -1 |
x + 2y | -3 > -4 (thỏa mãn) | -4 = -4 (thỏa mãn) | -5 < -4 (loại) |
Vậy miền nghiệm chứa hai điểm (x; y) $\in$ {(-1; -1); (-2; -1)} với x, y là các số nguyên âm.
Bài tập 2.5. Một cửa hàng bán lẻ bán hai loại hạt cà phê. Loại thứ nhất giá 140 nghìn đồng/kg và loại thứ hai giá 180 nghìn đồng/kg. Cửa hàng trộn x kg loại thứ nhất và y kg loại thứ hai sao cho hạt cà phê đã trộn có giá không quá 170 nghìn đồng/kg.
a) Viết bất phương trinh bậc nhất hai ẩn x, y thoả mãn điều kiện đề bài.
b) Biểu diễn miền nghiệm của bất phương trình tìm được ở câu a trên mặt phẳng toạ độ.
Trả lời:
a) Giá tiền của x kg cà phê loại thứ nhất là 140x (nghìn đồng).
Giá tiền của y kg cà phê loại thứ hai là 180y (nghìn đồng).
Tổng số tiền khi trộn x kg loại thứ nhất và y kg loại thứ hai là: 140x + 180y (nghìn đồng).
Tổng số kg cà phê sau khi trộn x kg loại thứ nhất và y kg loại thứ hai là: x + y (kg).
Giá của cà phê sau khi trộn có giá cao nhất là 170 nghìn đồng/kg nên số tiền cao nhất thu được khi bán x + y kg cà phê là 170(x + y) (nghìn đồng).
Khi đó ta có bất phương trình 140x + 180y $\leq$ 170(x + y).
$\Rightarrow$ 140x - 170x + 180y - 170y ≤ 0 $\Rightarrow$ -30x + 10y ≤ 0 $\Rightarrow$ -3x + y ≤ 0
Vậy bất phương trình bậc nhất hai ẩn x, y thỏa mãn điều kiện đề bài là -3x + y ≤ 0.
b) Xác định hai điểm thuộc đường thẳng d: -3x + y = 0.
x | 0 | 1 |
y | 0 | 3 |
Do đó đường thẳng d: -3x + y = 0 đi qua hai điểm có tọa độ (0; 0) và (1; 3).
Chọn điểm (0; 1) là điểm không thuộc đường thẳng d: -3x + y = 0 và thay vào biểu thức -3x + y ta có -3 . 0 + 1 = 1 > 0.
Do đó miền nghiệm của bất phương trình -3x + y ≤ 0 là nửa mặt phẳng bờ d không chứa điểm (0; 1) (miền không được gạch).

Ngoài giải bài tập Toán lớp 10 Kết Nối Tri Thức của Giaibaitapsgk sẽ cung cấp đầy đủ từng bước trong bài giải vở bài tập Toán lớp 10. Dựa vào đó các em cũng có thể nhận ra những điểm sai hoặc thiếu của mình khi làm bài và chủ động sửa đổi.
Toàn bộ hướng dẫn giải bài tập Toán lớp 10 sách Kết Nối Tri Thức sẽ là tài liệu hữu ích giúp các em học sinh rút ngắn thời gian làm bài tập về nhà, bậc phụ huynh có thể hiểu được cách giải Toán 10theo chương trình mới. Song song với đó Giaibaitapsgk cũng cung cấp bộ câu hỏi trắc nghiệm, phiếu bài tập cuối tuần để thầy cô, phụ huynh tham khảo giúp con có thêm cơ hội rèn luyện với nhiều dạng Toán lớp 10 nâng cao khác nhau.
