Phát triển từ đề thi minh họa THPT Quốc gia lần 3 môn Toán

20 chuyên đề Toán lớp 12 được Trang tài liệu liệt kê qua từng dạng bài tập giúp bồi dưỡng các em học sinh giỏi Toán lớp 12. Mời các bạn tham khảo

Đây là một số bài tập phát triển từ đề minh họa THPT lần 3 của Bộ giáo dục- đề thi được đánh giá là sát với đề thi thật nhất.

Ví dụ 1: Cho số phức z thỏa mãn điều kiện $|z-1-i|+|z-3-2i|=\sqrt{5}$. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của mô đun của z. Tính M+m.

A. $\frac{\sqrt{5}+5 \sqrt{13}}{5}$.

B. $\sqrt{5}+5 \sqrt{13}$.

C. $\sqrt{2}+\sqrt{13}$.

D. $\sqrt{2}+2 \sqrt{13}$.

 Giải: Đáp án C

Gọi $z=x+yi, (x, y \in \mathbb{R})$ có điểm M (x,y) biểu diễn số phức z trên mặt phẳng tọa độ.

Ta có $|z-1-i|+|z-3-2i|=\sqrt{5}$.

$\Leftrightarrow \sqrt{(x-1)^{2}+(y-1)^{2}}+\sqrt{(x-3)^{2}+(y-2)^{2}}=\sqrt{5}(1)$.

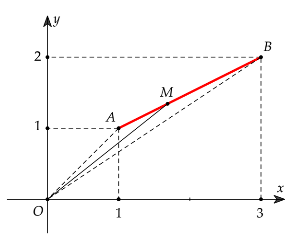
Đặt A(1,1), B(3,2) thì từ (1) ta có: $AM+BM=\sqrt{5} (2)$.

Mặt khác $\overrightarrow{AB}=(2,1) \Rightarrow AB = \sqrt{5}$ nên M thuộc AB.

Cách 1: Sử dụng hình vẽ 

Nhận xét rằng $\widehat{OAB}$ là góc tù ta có $M=|z_{\max}|=OB=\sqrt{13}$ và $m=|z|_{\min}=OA=\sqrt{2}$.

Vậy $M+m=\sqrt{2}+\sqrt{13}$.

Nhận xét: Một sai lầm thường gặp là đánh giá $|z|_{min}=d(O,AB)=\frac{\sqrt{5}}{5}$ nhưng do góc $\widehat{OAB}$ là góc tù nên không tồn tại điểm M trên đoạn AB sao cho $ OM \perp AB$.

Cách 2: Sử dụng hàm số

Ta có phương trình đoạn thẳng AB: x-2y+1=0 với $x \in [1,3], y \in [1,2]$.

$|z|=\sqrt{x^{2}+y^{2}}=\sqrt{(2y-1)^{2}+y^{2}}=\sqrt{5y^{2}-4y+1}$.

Xét hàm số $f(y)=5y^{2}-4y+1$ với $y\in [1,2].$

$f_{\max}=13, f_{\min}=2$. Suy ra $m=\sqrt{2}, M=\sqrt{13}$.

Ngoài ra, các bạn có thể tham khảo thêm nhiều dạng bài tập của nhiều chuyên đề khác nhau được Trang tài liệu liệt kê dưới đây nhé!

Ngoài 20 chuyên đề bồi dưỡng Toán 122. Các bạn học sinh còn có thể tham khảo thêm giải bài tập Toán lớp 12, giải vở bài tập Toán 12, soạn bài 12 hoặc đề thi lớp 12 học kì 1 và kì 2. Mong rằng với những gợi ý dưới đây của Trang tài liệu có thể giúp các em rèn luyện tốt khả năng làm và luyện đề