Chuyên đề tích phân chống Casio
20 chuyên đề Toán lớp 12 được Trang tài liệu liệt kê qua từng dạng bài tập giúp bồi dưỡng các em học sinh giỏi Toán lớp 12. Mời các bạn tham khảo
Phương pháp chung:
Cách 1: Giải theo hình thức tự luận
- Bước 1: Tính tích phân như bình thường.
- Bước 2: Dựa vào yêu cầu đề bài và làm tiếp.
Cách 2: Sử dụng máy tính
Ví dụ 1: Cho tích phân $I=\int_{0}^{\frac{\pi}{2}}e^{\sin ^{2}x}\sin x \cos^{3}xdx$. Nếu đổi biến $t=\sin ^{2} x$ thì
A. $I=\frac{1}{2}\int_{0}^{1}e^{t}(1-t)dt$.
B. $I=2 [\int_{0}^{1}e^{t}dt + \int_{0}^{1}te^{t}dt]$.
C. $I=2\int_{0}^{1}e^{t}(1-t)dt$.
D. $I=\frac{1}{2}[\int_{0}^{1}e^{t}dt+\int_{0}^{1}te^{t}dt]$.
Giải: Đáp án A
Cách 1: Theo tự luận
Đặt $t=\sin ^{2} x \Rightarrow dt=2\sin x \cos x dx$
Đổi cận $x=0 \Rightarrow t=0$, $x=\frac{\pi}{2} \Rightarrow t=1$.
Vậy $I=\frac{1}{2}\int_{0}^{1}e^{t}(1-t)dt$.
Cách 2: Ta chỉ cần tính tích phân đề bài cho và tích phân đáp án. Nếu trừ nhau bằng 0 thì là đáp án đúng.
Tính $I=\int_{0}^{\frac{\pi}{2}}e^{\sin ^{2}x}\sin x \cos^{3}xdx$

Tính tích phân ở đáp án A, B, C. Ở đáp án A

Ví dụ 2: Giả sử rằng $I=\int_{-2}^{0}\frac{3x^{2}+5x-1}{x-2}dx =a \ln \frac{2}{3}+b$. Khi đó giá trị của a+2b là
A. 30.
B. 40.
C. 50.
D. 60.
Giải: Đáp án B
Cách 1: Tự làm (chia phân tử cho mẫu số)
Cách 2: Sử dụng máy tính
Trước hết tính tích phân $I=\int_{-2}^{0}\frac{3x^{2}+5x-1}{x-2}dx =a \ln \frac{2}{3}+b$ và gán cho A

Lúc này chỉ việc giải hệ phương trình với a+2b ở các đáp án. Kết quả nào đẹp thì ta lấy đáp án đó
Đáp án A
Đáp án B

Đáp án C

Đáp án D

Ví dụ 3: Giả sử $I=\int_{1}^{5}\frac{1}{x\sqrt{3x+1}}dx=a\ln 3+b \ln 5$. Khi đó giá trị của $a^{2}+ab+4b^{2}$ là
A. 6.
B. 9.
C. 8.
D. 11.
Giải: Đáp án A
Cách 1: Đặt ẩn $t=\sqrt{3x+1}$.
Cách 2: Sử dụng máy tính
Trước hết tính tích phân gán cho A

Do vế phải của tích phân đều biểu diễn dưới dạng ln nên chắc chắn rằng tích phân đó cũng theo ln. Vì thế có $A=\ln x \Leftrightarrow X=e^{A}.$. Tính giá trị của biểu thức $e^{A}$
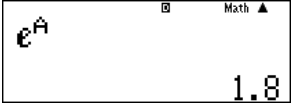
Vậy $X=\frac{9}{5}$. Do đó $\ln \frac{9}{5}=2 \ln 3 -\ln 5$ hay $a=2, b=-1$.
Ví dụ 4: Giả sử $\int_{0}^{\frac{1}{2}}\sqrt{1-x^{2}}dx=\frac{\sqrt{3}}{a}+\frac{\pi}{b}$ với $a, b \in \mathbb{Z}$. Khi đó giá trị của $\sqrt[3]{a}+2b$ là
A. 26.
B. 28.
C. 24.
D. 20.
Giải: Đáp án D
Áp dụng công thức tính gần đúng giá trị tích phân để dự đoán hệ số $\int_{a}^{b}f(x)dx\approx \frac{b-a}{2}(f(a)+f(b))$ (sử dụng khi $b-a \leq 1$)
Khi đó $\int_{0}^{\frac{1}{2}}\sqrt{1-x^{2}}dx \approx \frac{1}{4}(1+\sqrt{1-\frac{1}{4}})=\frac{\sqrt{3}}{8}+\frac{1}{4}$
Ta chỉ quan tâm tới phần $\sqrt{3}$ vì giả thiết bài toán cho và dự đoán a=8 và đi tìm b.
Tính tích phân và gán cho A

Do $A=\frac{\sqrt{3}}{8}+\frac{\pi}{b}$ nên b=12.
Lưu ý: Các bài toán trên mình khuyến khích nên giải tự luận sẽ nhanh hơn trừ một số bài thực sự phức tạp.

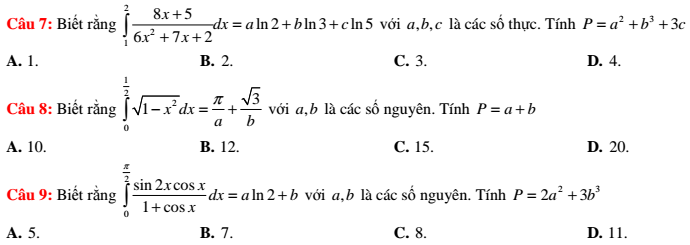
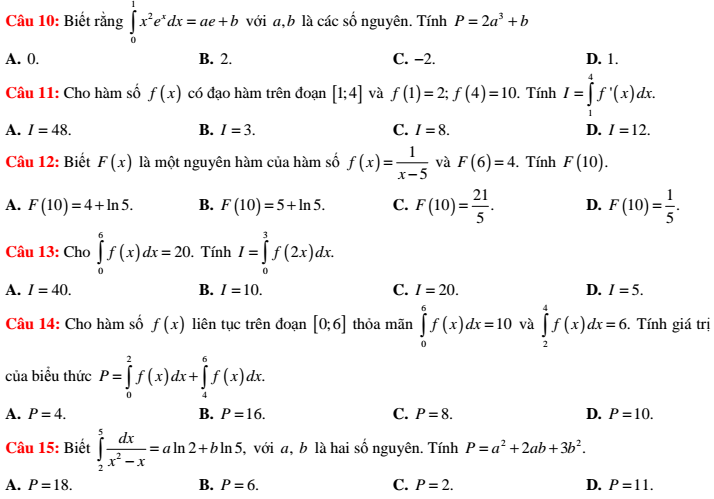
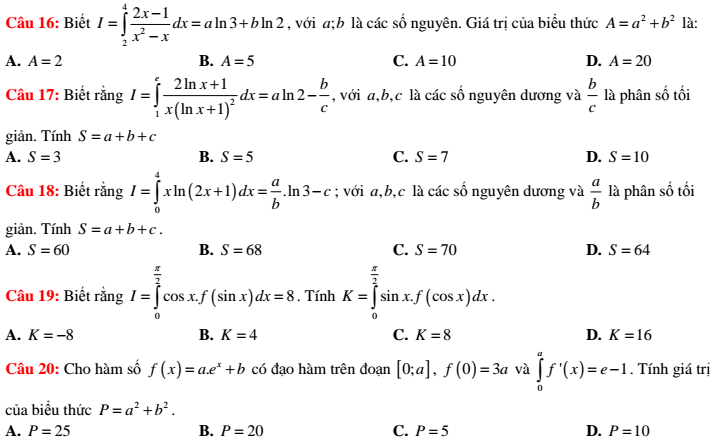
Ngoài ra, các bạn có thể tham khảo thêm nhiều dạng bài tập của nhiều chuyên đề khác nhau được Trang tài liệu liệt kê dưới đây nhé!
Ngoài 20 chuyên đề bồi dưỡng Toán 122. Các bạn học sinh còn có thể tham khảo thêm giải bài tập Toán lớp 12, giải vở bài tập Toán 12, soạn bài 12 hoặc đề thi lớp 12 học kì 1 và kì 2. Mong rằng với những gợi ý dưới đây của Trang tài liệu có thể giúp các em rèn luyện tốt khả năng làm và luyện đề
