Trắc nghiệm Toán 10 chân trời bài tập cuối chương III

Bài trắc nghiệm có đáp án. Câu hỏi và bài tập trắc nghiệm Toán 10 bài tập cuối chương III - sách chân trời sáng tạo. Học sinh luyện tập bằng cách chọn đáp án của mình trong từng câu hỏi. Dưới cùng của bài trắc nghiệm, có phần xem kết quả để biết bài làm của mình. Kéo xuống dưới để bắt đầu.

Câu 1: Cho hàm số $y = 2x^{2} – 4x + 3$ có đồ thị là parabol (P). Mệnh đề nào sau đây sai?

• A. (P) không có giao điểm với trục hoành;
• B. (P) có đỉnh là S(1;1);

• C. (P) có trục đối xứng là đường thẳng y = 1;

• D. (P) đi qua điểm M(‒1;9).

Câu 2: Cho hàm số $f(x) = 2x^{2} + ax + b$ (với a, b là tham số) thoả mãn f(2) = 11, f(3) = ‒7. Giá trị của 5a + 2b bằng:

• A. ‒26;

• B. ‒22;

• C. 4;
• D. 22.

Câu 3: Đồ thị dưới đây là của hàm số nào?

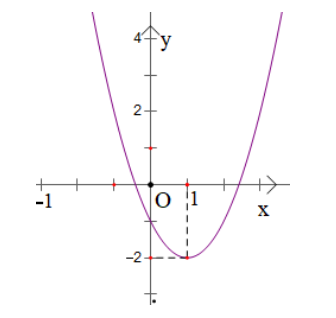
• A. y = ‒x$^{2}$ ‒2x + 3;
• B. y = x$^{2}$ + 2x – 2;
• C. y = 2x$^{2}$ – 4x – 2;

• D. y = x$^{2}$ – 2x – 1.

Câu 4: Cho hàm số y = 4x – 5 với x ∈ ℤ. Có bao nhiêu giá trị nguyên của x để ‒3 < y ≤ 10?

• A. 2;

• B. 3;

• C. 4;
• D. 5.

Câu 5: Tập xác định của hàm số $y=\frac{5-x}{x^{2}-2x}$ là:

• A. D = ℝ \ {0; 2};

• B. D = ℝ \ {0; 2; 5};
• C. D = ℝ \ (0; 2);
• D. D = ℝ \ [0; 2];

Câu 6: Cho hàm số y = 2x$^{2}$ – 4x + 2. Chọn khẳng định sai:

• A. Đồ thị hàm số đi qua điểm O(0; 0);

• B. Đồ thị hàm số có đỉnh S(1; 0);
• C. Đồ thị hàm số có trục đối xứng là x = 1;
• D. Hàm số có tập xác định là D = ℝ.

Câu 7: Theo tài liệu dân số và phát triển của Tổng cục dân số và kế hoạch hóa gia đình thì:

Dựa trên số liệu về dân số, kinh tế, xã hội của 85 nước trên thế giới, người ta xây dựng được hàm nêu lên mối quan hệ giữa tuổi thọ trung bình của phụ nữ (y) và tỷ lệ biết chữ của họ (x) như sau: y = 47,17 + 0,307x. Trong đó y là số năm (tuổi thọ), x là tỷ lệ phần trăm biết chữ của phụ nữ. Theo báo cáo của Bộ Giáo dục và Đào tạo năm học 2015 ‒ 2016, tỷ lệ biết chữ đã đạt 96,83% trong nhóm phụ nữ Việt Nam tuổi từ 15 đến 60. Hỏi với tỷ lệ biết chữ của phụ nữ Việt Nam như trên thì nhóm này có tuổi thọ bao nhiêu?

• A. 67,89 tuổi;

• B. 76,89 tuổi;

• C. 76,98 tuổi;
• D. 77,01 tuổi.

Câu 8: Khi quả bóng được đá lên, nó sẽ đạt độ cao nào đó rồi rơi xuống đất. Biết rằng quỹ đạo của quả là một cung parabol trong mặt phẳng với hệ tọa độ Oth , trong đó t là thời gian, kể từ khi quả bóng được đá lên: h là độ cao của quả bóng. Giả thiết rằng quả bóng được đá lên từ độ cao 1,2m. Sau đó 1 giây, nó đạt độ cao 8,5m và 2 giây sau khi đá lên, nó ở độ cao 6m. Hãy tì hàm số bậc hai biểu thị độ cao h theo thời gian t và có phần đồ thị trùng với quỹ đạo của quả bóng trong tình huống trên.

• A. y = 4,9t$^{2}$ + 12,2t + 1,2;

• B. y = ‒4,9t$^{2}$ + 12,2t + 1,2;

• C. y = ‒4,9t$^{2}$ + 12,2t ‒ 1,2;
• D. y = ‒4,9t$^{2}$ ‒ 12,2t + 1,2.

Câu 9: Một chiếc cổng hình parabol có dạng đồ thị giống đồ thị hàm số y = $-\frac{1}{2}x^{2}$ như hình vẽ. Cổng có chiều rộng d = 8 m. Tính chiều cao h của cổng.

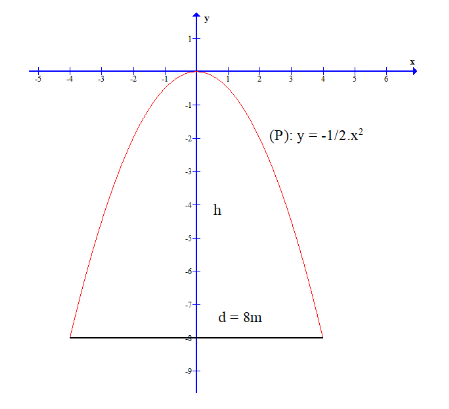
• A. h = 4m

• B. h = 8m

• C. h = 10m
• D. h = 16m

Câu 10: Cho hàm số có đồ thị như hình bên dưới.

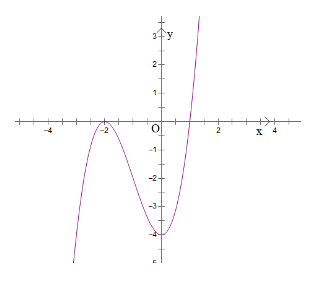
• A. Hàm số nghịch biến trên khoảng (‒2; 1);
• B. Hàm số đồng biến trên khoảng (‒∞; 1);

• C. Hàm số nghịch biến trên khoảng (‒2; 0);

• D. Hàm số đồng biến trên khoảng (‒∞; 0).

Câu 11: Cho hàm số y = (m – 1)x$^{2}$ – 2(m – 2)x + m – 3 (với m ≠ 1) (P). Đỉnh của (P) là S(‒1; ‒2) thì m có giá trị bằng:

• A. $\frac{3}{2}$

• B. 0
• C. $\frac{2}{3}$
• D. $\frac{1}{3}$

Câu 12: Cho hàm số $y=x\sqrt{m^{2}+2022}+m$ với x là biến số, m là tham số. Khẳng định nào sau đây là đúng?

• A. Nếu m > 0 thì hàm số đồng biến trên ℝ, nếu m < 0 thì hàm số nghịch biến trên ℝ;
• B. Nếu m > 0 thì hàm số nghịch biến trên ℝ, nếu m < 0 thì hàm số đồng biến trên ℝ;

• C. Với mọi m hàm số luôn đồng biến trên ℝ;

• D. Với mọi m hàm số luôn nghịch biến trên ℝ.

Câu 13: Cho hàm số $f(x)=x+\sqrt{x-3}$. Giá trị của f(f(4)) bằng:

• A. 4;
• B. 5;

• C.$5+\sqrt{2}$

• D.$5-\sqrt{2}$

Câu 14: Cho hàm số y = f(x) có tập xác định là [‒3; 3] và có đồ thị hàm số như hình vẽ.

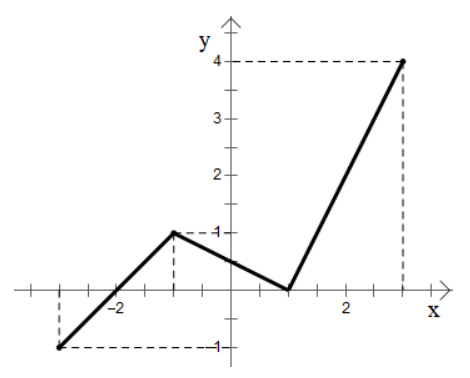
Khẳng định nào sau đây là đúng?

• A. Hàm số đồng biên trên khoảng (‒3; 1) và (1; 4);
• B. Hàm số nghịch biến trên khoảng (‒2; 1);

• C. Hàm số đồng biến trên khoảng (‒3; ‒1) và (1; 3);

• D. Đồ thị hàm số cắt trục hoành tại 3 điểm phân biệt.

Câu 15: Trục đối xứng của parabol y = ‒x2 + 5x + 3 là đường thẳng có phương trình:

• A. $x=\frac{5}{4}$
• B. $x=-\frac{5}{2}$
• C. $x=-\frac{5}{4}$

• D. $x=\frac{5}{2}$

Câu 16: Một chất điểm chuyển động chậm dần đều với vận tốc v = 16t – 2t (cm/s), thời gian đo bằng giây. Tại thời điểm nào chất điểm đạt vận tốc 6 cm/s?

• A. t = 2(s);
• B. t = 4 (s);

• C. t = 5 (s);

• D. t = 10 (s).

Câu 17: Cho hàm số y = ax$^{2}$ + bx + c có đồ thị như hình dưới đây.

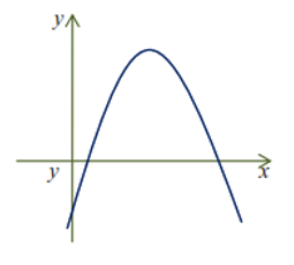
Khẳng định nào sau đây là đúng?

• A. a < 0, b > 0, c > 0;
• B. a > 0, b < 0, c > 0;

• C. a < 0, b > 0, c < 0;

• D. a > 0, b > 0, c < 0.

Câu 18: Một cửa hàng buôn giày nhập một đôi với giá là 40 đôla. Cửa hàng ước tính rằng nếu đôi giày được bán với giá x (x > 0) đôla thì mỗi tháng khách hàng sẽ mua (120 – x) đôi. Hỏi cửa hàng bán một đôi giày giá bao nhiều thì thu được nhiều lãi nhất?

• A. 80 USD;

• B. 160 USD;
• C. 40 USD;
• D. 240 USD.

Câu 19: Trong các điểm dưới đây, điểm nào thuộc đồ thị hàm số y = 2x$^{2}$ – x + 1

• A. M(0; 1);

• B. N(0; 0);
• C. P(1; 1);
• D. Q(2; 2).

Câu 20: Tìm tập xác định D của hàm số $y=f(x)=\sqrt{x+2022}+\frac{1}{x}$

• A. D = ℝ \ {0};
• B. D = ℝ \ {‒2022; 0};

• C. D = [‒2022; +∞) \{0};

• D. D = [‒2022; +∞).