Giải bài tập cuối chương II trang 31

Những bài học trong chương trình sách giáo khoa Toán lớp 10 đều được Giaibaitapsgk giải đáp chi tiết, cùng với đó là mục lục chi tiết theo từng chương và bài học cụ thể giúp các em nhanh chóng tra cứu và đối chiếu đáp án bất cứ lúc nào. Không chỉ hướng dẫn giải phần bài tập luyện tập mà những câu hỏi liên quan đến bài giảng, tiếp cận vấn đề cũng được chúng tôi giải đáp chi tiết, dễ hiểu và dễ ứng dụng.

Giải bài: Bài tập cuối chương II - sách kết nối tri thức toán 10 tập 1. Phần đáp án chuẩn, hướng dẫn giải chi tiết cho từng bài tập có trong chương trình học của sách giáo khoa. Hi vọng, các em học sinh hiểu và nắm vững kiến thức bài học.

A. TRẮC NGHIỆM

Bài tập 2.7. Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn?

A. x + y > 3                                    B. $x^{2}+ y^{2}\leq 4$

C. $(x – y)(3x + y) \geq 1$              D. $ y^{3}-2\leq 0$

Hướng dẫn giải:

Đáp án A

Bài tập 2.8. Cho bất phương trình 2x + y > 3. Khẳng định nào sau đây là đúng?

A. Bất phương trình đã cho có nghiệm duy nhất.

B. Bất phương trình đã cho vô nghiệm.

C. Bất phương trình đã cho có vô số nghiệm

D. Bất phương trình đã cho có tập nghiệm là $ [3;+\infty )$.

Hướng dẫn giải:

Đáp án C

Bài tập 2.9. Hình nào sau đây biểu diễn miền nghiệm của bất phương trình x – y < 3?

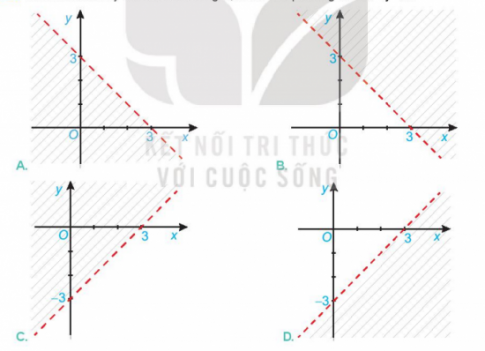
Hướng dẫn giải:

Đáp án D

Bài tập 2.10. Hệ bất phương trình nào sau đây là hệ bất phương trình bậc nhất hai ẩn?

A. $ \left\{\begin{matrix}x-y<0\\ 2y\geq 0\end{matrix}\right.$

B. $ \left\{\begin{matrix}3x+y^{3}<0\\ x+y>3\end{matrix}\right.$

C. $\left\{\begin{matrix}x+2y<0\\ y^{2}+3< 0\end{matrix}\right.$

D. $\left\{\begin{matrix}-x^{3}+y<4\\ x+2y<1\end{matrix}\right.$

Hướng dẫn giải:

Đáp án A

Bài tập 2.11. Cho hệ bất phương trình $ \left\{\begin{matrix}x-y<-3\\ 2y\geq -4\end{matrix}\right.$. Điểm nào sau đây thuộc miền nghiệm của hệ đã cho?

A. (0; 0)                  B. (-2; 1)                    C. (3; -1)                      D. (-3; 1)

Hướng dẫn giải:

Đáp án D

Tham khảo hướng dẫn giải vở bài tập Toán lớp, bộ tài liệu giúp các em nhanh chóng hoàn thành bài tập về nhà của mình. Đồng thời nắm được cách giải những dạng toán quen thuộc.

Đừng quên theo dõi website của chúng tôi để cập nhật thường xuyên những tài liệu học tốt môn Toán 10 hấp dẫn khác ngoài giải Toán lớp 10 Kết Nối Tri Thức: Toán cơ bản và năng cao lớp 10, Toán, Tiếng Anh 10,... Tham khảo bộ tài liệu sẽ giúp các em tiếp cận với những dạng toán nâng cao và trinh phục điểm 10 môn Toán trọn vẹn, cũng như thường xuyên ôn tập nắm chắc dạng Toán cơ bản.