Giải bài 2 Tập hợp và các phép toán trên tập hợp
Những bài học trong chương trình sách giáo khoa Toán lớp 10 đều được Giaibaitapsgk giải đáp chi tiết, cùng với đó là mục lục chi tiết theo từng chương và bài học cụ thể giúp các em nhanh chóng tra cứu và đối chiếu đáp án bất cứ lúc nào. Không chỉ hướng dẫn giải phần bài tập luyện tập mà những câu hỏi liên quan đến bài giảng, tiếp cận vấn đề cũng được chúng tôi giải đáp chi tiết, dễ hiểu và dễ ứng dụng.
Giải bài 2: Tập hợp và các phép toán trên tập hợp - sách kết nối tri thức toán 10 tập 1. Phần đáp án chuẩn, hướng dẫn giải chi tiết cho từng bài tập có trong chương trình học của sách giáo khoa. Hi vọng, các em học sinh hiểu và nắm vững kiến thức bài học.
1. Các khái niệm cơ bản về tập hợp
a) Tập hợp
Hoạt động 1: Trong tình huống trên, gọi A là tập hợp những thành viên tham gia Chuyên đề 1, B là tập hợp những thành viên tham gia Chuyên đề 2.
a. Nam có là một phần tử của tập hợp A không? Ngân có là một phần tử của tập hợp B không?
b. Hãy mô tả các tập hợp A và B bằng cách liệt kê các phần tử.
Hướng dẫn giải:
a.
- Nam có là phần tử của tập hợp A.
- Ngân không là phần tử của tập hợp B.
b.
- Tập hợp A= {Nam; Hương; Tú; Khánh; Bình; Chi; Ngân}
- Tập hợp B = {Hương; Khánh; Hiền; Chi; Bình; Lam; Tú; Hân}
Hoạt động 2: Cho tập hợp:
C = {châu Á; châu Âu; châu Đại Dương; châu Mĩ; châu Nam Cực; châu Phi}.
a. Hãy chỉ ra tính chất đặc trưng cho các phần tử của tập hợp C.
b. Tập hợp C có bao nhiêu phần tử?
Hướng dẫn giải:
a. Tính chất đặc trưng của các phần tử C: các châu luc trên Trái Đất.
b. Tập hợp C có 6 phần tử.
Luyện tập 1: Gọi X là tập nghiệm của phương trình x2 – 24x + 143 = 0.
Các mệnh đề sau đúng hay sai?
a. 13 $ \in$ X b. 11 $ \notin$ X c. n(X) = 2.
Hướng dẫn giải:
a. mệnh đề đúng
b. mệnh đề sai
c. mệnh đề đúng
b) Tập hợp con
Hoạt động 3: Gọi H là tập hợp các bạn tham gia Chuyên đề 2 trong tình huống mở đầu có tên bắt đầu bằng chữ H. Các phần tử của tập hợp H có là phần tư của tập hợp B trong HĐ1 không?
Hướng dẫn giải:
Phần tử của H là phần tử của B.
c) Hai tập hợp bằng nhau
Hoạt động 4: Sơn và Thu viết tập hợp các số chính phương nhỏ hơn 100 như sau:
Sơn: S = {0; 1; 4; 9; 16; 25; 36; 49; 64; 81}
Thu: T = { $n\in \mathbb{N}|n$ là số chính phương; n < 100}.
Hỏi bạn nào viết đúng?
Hướng dẫn giải:
Bạn Thu viết đúng.
Luyện tập 2: Giả sử C là tập hợp các hình bình hành có hai đường chéo vuông góc; D là tập hợp các hình vuông.
Các mệnh đề sau đúng hay sai?
a. $C\subset D$ b. $C \supset D$ c. C = D.
Hướng dẫn giải:
- Mệnh đề đúng: b.
- Mệnh đề sai: a, c.
2. Các tập hợp số
a) Mối quan hệ giữa các tập hợp số:
Hoạt động 5: Các mệnh đề sau đúng hay sai?
a. Mọi số nguyên đều viết được dưới dạng phân số
b. Tập hợp các số thực chứa tập hợp các số hữu tỉ
c. Tồn tại một số thực không là số hữu tỉ.
Hướng dẫn giải:
Mệnh đề đúng: a, b, c.
Luyện tập 3: Cho tập hợp C = {-4; 0; 1; 2}. Các mệnh đề sau đúng hay sai?
a. C là tập con của $\mathbb{Z}$ b. C là tập con của $\mathbb{N}$ c. C là tập con của $\mathbb{R}$
Hướng dẫn giải:
- Mệnh đề đúng: a, c.
- Mệnh đề sai: b.
b) Các tập con thường dùng của $\mathbb{R}$
Hoạt động 6: Cho hai tập hợp C = {$ x\in \mathbb{R}|x\geq 3$} và D = { $x\in \mathbb{R}|x> 3$}.
Các mệnh đề sau đúng hay sai?
a. C, D là các tập con của $\mathbb{R}$
b. $\forall x,x\in C\Rightarrow x\in D$
c. $3\Rightarrow C$ nhưng $\Rightarrow$
d. C = D.
Hướng dẫn giải:
- Mệnh đề đúng: a, c.
- Mệnh đề sai: b, d.
Luyện tập 4: Hãy ghép mỗi dòng ở cột bên trái với một dòng thích hợp ở cột bên phải.

Hướng dẫn giải:
1 – d
2 – a
3 – b
4 – c
3. Các phép toán trên tập hợp
a) Giao của hai tập hợp
Hoạt động 7: Viết tập hợp X gồm những thành viên tham gia cả hai chuyên đề 1 và 2 trong tình huống mở đầu.
Tập X có phải là tập con của tập A không? Tập X có phải là tập con của tập hợp B không? (A, B là các tập hợp trong HĐ 1)
Hướng dẫn giải:
X = {Khánh; Hương; Tú; Bình; Chi}
Tập hợp X là tập con của A và B.
Luyện tập 5: Cho các tập hợp C = [1; 5], D = [-2; 3]. Hãy xác định tập hợp $C \cap D$.
Hướng dẫn giải:
$C \cap D = [3; 5]$.
b) Hợp của hai tập hợp
Hoạt động 8: Trở lại tình huống mở đầu, hãy xác định tập hợp các thành viên tham gia Chuyên đề 1 hoặc Chuyên đề 2.
Hướng dẫn giải:
Tập hợp các thành viên tham gia Chuyên đề 1 hoặc Chuyên đề 2: {Nam; Tú; Khánh; Hương; Bình; Chi; Ngân; Hiền; Lam; Hân}.
Luyện tập 6: Hãy biểu diễn tập hợp $A\cup B$ bằng biểu đồ Ven, với A, B được cho trong HĐ 1.
Hướng dẫn giải:
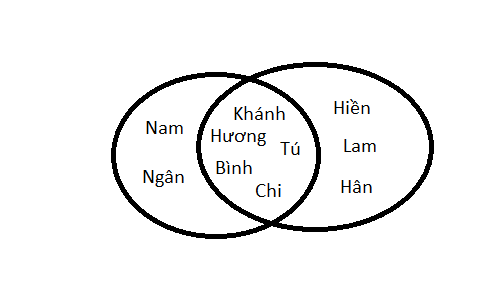
c) Hiệu của hai tập hợp
Hoạt động 9: Trở lại tình huống mở đầu, hãy xác định tập hợp các thành viên chỉ tham gia Chuyên đề 1 mà không tham gia Chuyên đề 2.
Hướng dẫn giải:
Các thành viên chỉ tham gia Chuyên đề 1 mà không tham gia Chuyên đề 2: Nam, Ngân.
Luyện tập 7: Tìm phần bù của các tập hợp sau trong $\mathbb{R}$.
a. $(-\infty ;-2)$ b. $[-5;+\infty )$
Hướng dẫn giải:
a. $[-2;+\infty )$
b. $(-\infty ;-5)$
Vận dụng: Lớp 10A có 24 bạn tham gia thi đấu bóng đá và cầu lông, trong đó có 16 bạn thi đấu bóng đá và 11 bạn thi đấu cầu lông. Giả sử các trận bóng đá và cầu lông không tổ chức đồng thời. Hỏi có bao nhiêu bạn lớp 10A tham gia thi đâu cả bóng đá và cầu lông?
Hướng dẫn giải:
A là tập hợp các bạn thi đấu bóng đá.
B là tập hợp các bạn thi đấu cầu lông.
Thì số bạn tham gia thi đấu cả bóng đá và cầu lông chính là số phần tử của tập hợp $ A\cap B$.
Ta có: $n(A\cup B)=n(A)+n(B)-n(A\cap B)$
24 = 16 + 11 - $ n(A\cap B)$
Suy ra: $ n(A\cap B)$ = 3.
Vậy có 3 bạn vừa thi đấu bóng đá vừa thi đấu cầu lông.
Tham khảo hướng dẫn giải vở bài tập Toán lớp, bộ tài liệu giúp các em nhanh chóng hoàn thành bài tập về nhà của mình. Đồng thời nắm được cách giải những dạng toán quen thuộc.
Đừng quên theo dõi website của chúng tôi để cập nhật thường xuyên những tài liệu học tốt môn Toán 10 hấp dẫn khác ngoài giải Toán lớp 10 Kết Nối Tri Thức: Toán cơ bản và năng cao lớp 10, Toán, Tiếng Anh 10,... Tham khảo bộ tài liệu sẽ giúp các em tiếp cận với những dạng toán nâng cao và trinh phục điểm 10 môn Toán trọn vẹn, cũng như thường xuyên ôn tập nắm chắc dạng Toán cơ bản.
