Giải bài 4 Hệ bất phương trình bậc nhất hai ẩn

Những bài học trong chương trình sách giáo khoa Toán lớp 10 đều được Giaibaitapsgk giải đáp chi tiết, cùng với đó là mục lục chi tiết theo từng chương và bài học cụ thể giúp các em nhanh chóng tra cứu và đối chiếu đáp án bất cứ lúc nào. Không chỉ hướng dẫn giải phần bài tập luyện tập mà những câu hỏi liên quan đến bài giảng, tiếp cận vấn đề cũng được chúng tôi giải đáp chi tiết, dễ hiểu và dễ ứng dụng.

Giải bài 4: Hệ bất phương trình bậc nhất hai ẩn - sách kết nối tri thức toán 10 tập 1. Phần đáp án chuẩn, hướng dẫn giải chi tiết cho từng bài tập có trong chương trình học của sách giáo khoa. Hi vọng, các em học sinh hiểu và nắm vững kiến thức bài học.

1. HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN

Hoạt động 1: Trong tình huống mở đầu, gọi x và y lần lượt là số máy điều hòa loại hai chiều và một chiều mà cửa hàng cần nhập. Tính số tiền vốn mà cửa hàng phải bỏ ra để nhập hai loại máy điều hòa theo x và y.

a. Do nhu cầu của thị trường không quá 100 máy nên x và y cần thỏa mãn điều kiện gì?

b. Vì số vốn mà chủ cửa hàng có thể đầu tư không vượt quá 1,2 tỉ đồng nên x và y phải thỏa mãn điều kiện gì?

c. Tính số tiền lãi mà cửa hàng dự kiến thu được theo x và y.

Hướng dẫn giải:

Số tiền vốn mà cửa hàng phải bỏ ra để nhập hai loại máy điều hòa theo x và y: 20x + 10y (triệu đồng).

a. x + y $\leq$ 100

b. 20x + 10y $\leq$ 1200

c. 3,5x + 2y

Luyện tập 1: Trong tình huống mở đầu, gọi x và y lần lượt là số máy điều hòa loại hai chiều và một chiều mà cửa hàng cần nhập. Từ HD1, viết hệ phương trình hai ẩn x, y và chỉ ra một nghiệm của hệ này.

Hướng dẫn giải:

Hệ bất phương trình:

$\left\{\begin{matrix}x\geq 0\\y\geq 0\\x+y\leq 100\\20x+10y\leq 1200\end{matrix}\right.$

Một nghiệm của hệ: (x; y) = (30; 20)

2. BIỂU DIỄN MIỀN NGHIỆM CỦA HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN TRÊN MẶT PHẲNG TỌA ĐỘ

Hoạt động 3: Cho đường thẳng d: x + y = 150 trên mặt phẳng tọa độ Oxy. Đường thẳng này cắt hai trục tọa độ Ox và Oy tại hai điểm A và B.

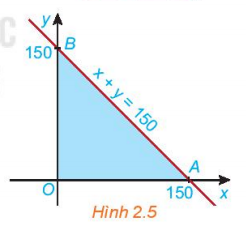
a. Xác định các miền nghiệm D₁,D₂, D₃ của bất phương trình tương ứng $ x\geq 0; y\geq 0$ và $ x+y\leq 150$.

b. Miền tam giác OAB có phải là giao của các miền D₁, D₂, D₃ hay không?

c. Lấy một điểm trong tam giác OAB và kiểm tra xem tọa độ của các điểm đó có phải là nghiệm của hệ bất phương trình sau hay không:
$\left\{\begin{matrix} x\geq 0\\y\geq 0\\x+y\leq 150\\\end{matrix}\right.$

Hướng dẫn giải:

a.

$ x\geq 0$: Miền nghiệm là nửa mặt phẳng bờ là trục Oy chứa điểm A, kể cả trục Oy.

$ y\geq 0$: Miền nghiệm là nửa mặt phẳng bờ là trục Ox chứa điểm B, kể cả trục Ox.

$ x+y\leq 150$: Miền nghiệm là nửa mặt phẳng bờ là đường thẳng d chứa điểm O, kể cả đường thẳng d.

b. Có là giao

c. Lấy điểm (3; 100) điểm này thõa mãn hệ bất phương trình đã cho.

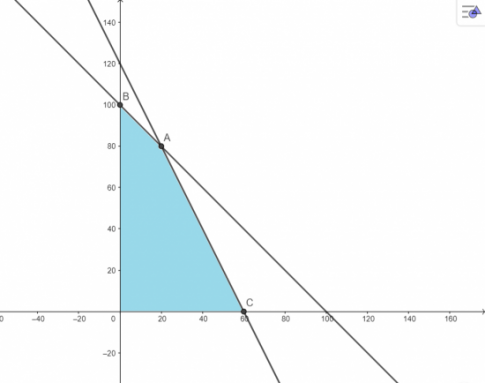
Luyện tập 2: Biểu diễn miền nghiệm của hệ bất phương trình bậc nhất hai ẩn sau trên mặt phẳng tọa độ:

$\left\{\begin{matrix}x\geq 0\\y\geq 0\\x+y\leq 100\\2x+y\leq 120\end{matrix}\right.$

Hướng dẫn giải:

Miền nghiệm của hệ bất phương trình là tứ giác OBAC, bỏ đi cạnh OC và AC.

Với O(0; 0), B(0; 100), A(20; 80), C(60; 0).

3. ỨNG DỤNG CỦA HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN

Hoạt động 3: Xét biểu thức F(x; y) = 2x + 3y với (x; y) thuộc miền tam giác OAB ở HD2. Tọa độ ba đỉnh là O(0; 0), A(150; 0) và B(0; 150).

a. Tính giá trị của biểu thức F(x; y) tại mỗi đỉnh O, A, B.

b. Nêu nhận xét về dấu của hoành độ x và tung độ y của điểm (x; y) nằm trong tam giác OAB. Từ đó suy ra giá trị nhỏ nhất của F(x; y) trên miền tam giác OAB.

c. Nêu nhận xét về tổng x + y của điểm (x; y) nằm trong miền tam giác OAB. Từ đó suy ra giá trị lớn nhất của F(x; y) trên miền tam giác OAB.

Hướng dẫn giải:

a.

O: F(0; 0) = 0

A: F(150; 0) = 300

B: F(0; 150) = 450

b. Nhận xét: x và y đều nhận giá trị không âm.

Giá trị nhỏ nhất của F(x; y) trên miền tam giác OAB là: 0 tại x = y = 0.

c. Nhận xét: x + y $\geq 0$ và $x+y \leq 300$

Giá trị lớn nhất của F(x; y) trên miền tam giác OAB là: 450 tại x = 0, y = 150.

Vận dụng: Một cửa hàng có kế hoạch nhập về hai loại máy tính A và B, giá mỗi chiếc lần lượt 10 triệu đồng và 20 triệu động với số vốn ban đầu không vượt quá 4 tỉ đồng. Loại máy A mang lại lợi nhuận 2,5 triệu đồng cho mỗi máy bán được và loại máy B mang lại lợi nhuận là 4 triệu đồng mỗi máy. Cửa hàng ước tính rằng tổng nhu cầu hàng tháng sẽ không vượt quá 250 máy. Giả sử trong một tháng cửa hàng cần nhập số máy tính loại A là x và số máy tính loại B là y.

a. Viết các bất phương trình biểu thị các điều kiện của bài toán thành một hệ bất phương trình rồi xác định miền nghiệm của hệ đó.

b. Gọi F (triệu đồng) là lợi nhuận mà cửa hàng thu được trong tháng đó khi bán x máy tính loại A và y máy tính loại B. Hãy biểu diễn F theo x và y.

c. Tìm số lượng máy tính mỗi loại cửa hàng cần nhập về trong tháng đó để lợi nhuận thu được là lớn nhất.

Hướng dẫn giải:

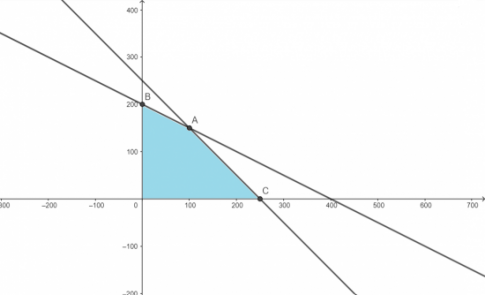
a. Hệ bất phương trình :

Gọi x và y lần lượt là số máy mà cửa hàng mua hai loại máy tính A và B trong một tháng ($x, y\in \mathbb{N}$).

$\left\{\begin{matrix}x\geq 0\\y\geq 0\\x+y\leq 250\\20x+10y\leq 4000\end{matrix}\right.$

b. F(x; y) = 2,5x + 4y

c.

• Miền nghiệm của hệ phương trình ở câu a là: miền của tứ giác OBAC với O(0; 0), B(0; 200), A( 100; 150), C(250; 0).
• Tính giá trị của biểu thức F tại các đỉnh của tứ giác trên, ta được giá trị lớn nhất cần tìm là F(100; 150) = 850.

Vậy cửa hàng cần mua 100 máy tính loại A và 150 máy tính loại B.

Tham khảo hướng dẫn giải vở bài tập Toán lớp, bộ tài liệu giúp các em nhanh chóng hoàn thành bài tập về nhà của mình. Đồng thời nắm được cách giải những dạng toán quen thuộc.

Đừng quên theo dõi website của chúng tôi để cập nhật thường xuyên những tài liệu học tốt môn Toán 10 hấp dẫn khác ngoài giải Toán lớp 10 Kết Nối Tri Thức: Toán cơ bản và năng cao lớp 10, Toán, Tiếng Anh 10,... Tham khảo bộ tài liệu sẽ giúp các em tiếp cận với những dạng toán nâng cao và trinh phục điểm 10 môn Toán trọn vẹn, cũng như thường xuyên ôn tập nắm chắc dạng Toán cơ bản.