Giải bài 3 Các phép toán trên tập hợp

Tất cả kiến thức, câu hỏi trong sách giáo khoa Toán lớp 10 Chân Trời Sáng Tạo đều được Giaibaitapsgk giải đáp chi tiết. Với mục lục được phân tách theo chương theo bài chi tiết các em học sinh có thể dễ dàng tra cứu đáp án và cách giải chi tiết. Tham khảo tài liệu này của chúng tôi sẽ giúp các em rút ngắn thời gian học tập, chuẩn bị bài mới và nhanh chóng xác định lại cách giải toán của mình có đúng hay không?

Giải bài 3: Các phép toán trên tập hợp - sách chân trời sáng tạo toán 10 tập 1. Phần đáp án chuẩn, hướng dẫn giải chi tiết cho từng bài tập có trong chương trình học của sách giáo khoa. Hi vọng, các em học sinh hiểu và nắm vững kiến thức bài học.

KHỞI ĐỘNG

Có hai đường tròn chia một hình chữ nhật thành các miền như hình bên. Hãy đặt mỗi thẻ số sau đây vào miền thích hợp trên hình chữ nhật và giải thích cách làm.

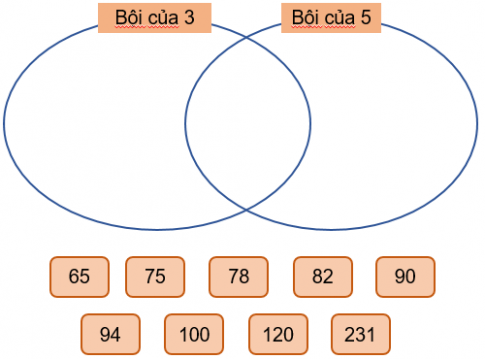
Hướng dẫn giải:

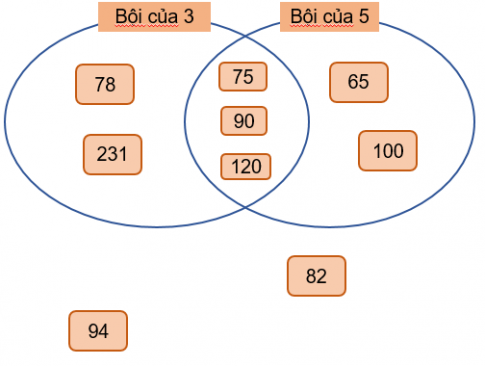
Giải thích: Số chia hết cho 3 là số có tổng các các chữ số chia hết cho 3, gắn vào miền Bội của 3". Số có tận cùng là 0 hoặc 5 thì chia hết cho 5, gắn vào miền chia hết cho 5. Những số vừa chia hết cho 3, vừa chia hết cho 5 thì gắn vào hai miền trùng nhau của "Bội của 3" và "Bội của 5".

1. HỢP VÀ GIAO CỦA CÁC TẬP HỢP

Khám phá 1: Bảng sau đây cho biết kết quả vòng phỏng vấn tuyển dụng vào một công ty (dấu "+" là đạt, dấu "-" là không đạt):

a. Xác định tập hợp A gồm các ứng viên đạt yêu cầu về chuyên môn, tập hợp B gồm các ứng viên đạt yêu cầu về ngoại ngữ.

b. Xác định tập hợp C gồm các ứng viên đạt yêu cầu cả về chuyên môn mà ngoại ngữ.

c. Xác định tập hợp D gồm các ứng viên đạt ít nhất một trong hai yêu cầu về chuyên môn và ngoại ngữ.

Hướng dẫn giải:

a. A = {$a_{1}$; $a_{2}$; $a_{5}$; $a_{6}$; $a_{7}$; $a_{8}$; $a_{10}$}

    B = {$a_{1}$; $a_{3}$; $a_{5}$; $a_{6}$; $a_{8}$; $a_{10}$}

b. C = {$a_{1}$; $a_{5}$; $a_{6}$; $a_{8}$; $a_{10}$}

c. D = {$a_{2}$; $a_{3}$; $a_{7}$}

Thực hành 1: Xác định các tập hợp A $\cup$ B và A $\cap$ B, biết:

a. A = {a; b; c; d; e}, B = {a; e; i; u}

b. A = {x $\in \mathbb{R}$ | $x^{2}$ + 2x - 3 = 0}, B = {x $\in \mathbb{R}$ | |x| = 1}

Hướng dẫn giải:

a. A $\cup$ B = {a; b; c; d; e; i; u}

A $\cap$ B = {a; e}

b. A $\cup$ B = {-3; -1; 1}

A $\cap$ B = {1}

Thực hành 2: Cho A = {(x; y) | x, y  $\in \mathbb{R}$, 3x - y = 9}, B = {(x; y) | x, y  $\in \mathbb{R}$, x - y = 1}. Hãy xác định A $\cap$ B.

Hướng dẫn giải:

A $\cap$ B = {(x; y) = (4; 3)}

Vận dụng: Tại vòng chung kết của một trò chơi trên truyền hình, có 100 khán giả tại trường quay có quyền bình chọn cho hai thí sinh A và B. Biết rằng có 85 khám giả bình chọn cho thí sinh A, 72 khán giả bình chọn cho thí sinh B và 60 khán giả bình chọn cho cả hai thí sinh này. Có bao nhiêu khán gải đã tham gia bình chọn? Có bao nhiêu khán giả không tham gia bình chọn?

Hướng dẫn giải:

• Số khán giả tham gia bình chọn là: 85 + 72 - 60 = 97 (khán giả)
• Số khán giả không tham gia bình chọn là: 100 - 97 = 3 (khán giả)

2. HIỆU CỦA HAI TẬP HỢP, PHẦN BÙ CỦA TẬP CON

Khám phá 2: Trở lại bảng thông tin về kết quả phỏng vấn tuyển dụng ở Khám phá 1.

a. Xác định tập hợp E gồm những ứng viên đạt yêu cầu về chuyên môn nhưng không đạt yêu cầu về ngoại ngữ.

b. Xác định tập hợp F gồm những ứng viên không đạt yêu cầu về chuyên môn.

Hướng dẫn giải:

a. E = {$a_{2}$; $a_{7}$}

b. F = {$a_{3}$; $a_{4}$; $a_{9}$}

Thực hành 3: Cho các tập hợp E = {x $\in \mathbb{N}$| x < 8}, A = {0; 1; 2; 3; 4}, B = {3; 4; 5}.

Xác định các tập hợp sau đây:

a. A\B, B\A và (A\B) $\cap$ (B\A);

b. $C_{E}$(A$\cap$B) và ($C_{E}$A) $\cup$ ($C_{E}$B)

c. $C_{E}$(A$\cup$B) và ($C_{E}$A) $\cap$ ($C_{E}$B)

Hướng dẫn giải:

a. A\B = {0; 1; 2}          B\A = {5}         (A\B) $\cap$ (B\A) = Ø

b. $C_{E}$(A$\cap$B) = {0; 1; 3; 5; 6; 7}

($C_{E}$A) $\cup$ ($C_{E}$B) = {0; 1; 2; 5; 6; 7}

c. $C_{E}$(A$\cup$B) = {6; 7}

($C_{E}$A) $\cap$ ($C_{E}$B) = {6; 7}

Thực hành 4: Xác định các tập hợp sau đây:

a. (1; 3) $\cup$ [-2; 2]

b. (-$\infty$; 1) $\cap$ [0; $\pi$]

c. [$\frac{1}{2}$; 3)\ (1; +$\infty$)

d. $C_{E}$[-1; +$\infty$)

Hướng dẫn giải:

a. [-2: 3)          b. [0; 1)          c. [$\frac{1}{2}$; 1)          d. (-$\infty$; -1)

Đừng quên dành thời gian thử sức với tài liệu Toán cơ bản và nâng cao lớp 10 của chúng tôi. Tài liệu sẽ giúp các em học sinh có thể nhanh chóng cập nhật kiến thức, từng bước chinh phục điểm 10 trọn vẹn.

Mong rằng những tài liệu mà chúng tôi cung cấp sẽ giúp các em học tập tốt môn Toán. Ngoài tài liệu giải Toán lớp 10 Giaibaitapsgk còn rất nhiều tài liệu học tốt hữu ích khác mà các em có thể tham khảo để nâng cao khả năng của mình: Trắc nghiệm Toán lớp 10, giải vở bài tập Toán lớp 10,...