Giải bài 2 Số thực. Giá trị tuyệt đối của một số thực
Với bộ tài liệu hướng dẫn giải Toán lớp 7 Chân Trời Sáng Tạo theo chương trình mới của Giaibaitapsgk các em học sinh có thể hoàn thành tốt chương trình học. Dựa vào việc nắm chắc công thức và rèn luyện những dạng toán đặc trưng: Toán lớp 7 số hữu tỉ, số thực, góc và các đường thẳng song song,....
Giải bài 2: Số thực. Giá trị tuyệt đối của một số thực - sách chân trời sáng tạo toán 7 tập 1. Phần đáp án chuẩn, hướng dẫn giải chi tiết cho từng bài tập có trong chương trình học của sách giáo khoa. Hi vọng, các em học sinh hiểu và nắm vững kiến thức bài học.
1. SỐ THỰC VÀ TẬP HỢP CÁC SỐ THỰC
Hoạt động khám phá 1: Trong các số sau, số nào là số hữu tỉ, số nào là số vô tỉ?
$\frac{2}{3}$ ; 3,(45) ; $\sqrt{2}$ ; -45 ; $-\sqrt{3}$ ; 0 ; π.
Hướng dẫn giải:
Có: 3,(45) = $\frac{38}{11}$ ; -45 = $\frac{-45}{1}$; 0 = $\frac{0}{1}$
$\sqrt{2}$ = 1,414... ; $-\sqrt{3}$ = -1,732... ; π = 3,1415..
=> Các số: $\frac{2}{3}$ ; 3,(45) ; -45 ; 0 là số hữu tỉ
Các số $\sqrt{2}$ ; $-\sqrt{3}$ ; π là số vô tỉ.
Thực hành 1: Các khẳng định sau đúng hay sai? Nếu sai, hãy phát biểu lại cho đúng.
a) $\sqrt{3}$ ∈ $\mathbb{Q}$
b) $\sqrt{3}$ ∈ $\mathbb{R}$
c) $\frac{2}{3}$ ∉ $\mathbb{R}$
d) -9 ∈ $\mathbb{R}
Hướng dẫn giải:
a) $\sqrt{3}$ ∈ $\mathbb{Q}$ . Sai
Sửa lại : $\sqrt{3}$ ∉ $\mathbb{Q}$
b) $\sqrt{3}$ ∈ $\mathbb{R}$ . Đúng
c) $\frac{2}{3}$ ∉ $\mathbb{R}$. Sai
Sửa lại : $\frac{2}{3}$ ∈ $\mathbb{R}$.
d) -9 ∈ $\mathbb{R}$. Đúng
2. THỨ TỰ TRONG TẬP HỢP CÁC SỐ THỰC
Hoạt động khám phá 2: Hãy so sánh các số thập phân sau đây: 3,14; 3,1415; 3,141515.
Hướng dẫn giải:
3,14 < 3,1415 < 3,141515.
Thực hành 2: So sánh hai số thực:
a) 4,(56) và 4,56279
b) -3,(65) và -3,6491
c) 0,(21) và 0,2(12)
d) $\sqrt{2}$ và 1,42
Hướng dẫn giải:
a) Có: 4,(56)= 4,5656….
Vì 4,5656… > 4,56279 => 4,(56) > 4,56279
b) Có: -3,(65) = -3,6565…
Vì -3,6565…> -3,6491. Do đó, -3,(65) < -3,6491;
c) Có: 0,(21) = $\frac{21}{99}$ = $\frac{7}{33}$ ; 0,2(12) = 0,2 + $\frac{12}{99}$ = $\frac{7}{33}$
Vận dụng 1: Cho một hình vuông có diện tích 5m2. Hãy so sánh độ dài a của cạnh hình vuông đó với độ dài b = 2,361m.
Hướng dẫn giải:
Độ dài của cạnh hình vuông có diện tích 5 m2 là: a = $\sqrt{5}$ $\approx$ 2,236 (cm)
Có 2,236.. < 2,361
=> a < b.
3. TRỤC SỐ THỰC
Hoạt động khám phá 3: Quan sát hình vẽ bên và cho biết độ dài của đoạn thẳng OA bằng bao nhiêu? Độ dài OA có là số hữu tỉ hay không?
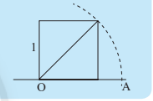
Hướng dẫn giải:
Đường chéo của hình vuông có độ dài đường chéo là 1 bằng $\sqrt{2}$ là số vô tỉ.
Thực hành 3: Hãy biểu diễn các số thực: -2; $-\sqrt{2}$ ; -1,5; 2; 3 trên trục số
Hướng dẫn giải:
Biểu diễn các số thực: -2; $-\sqrt{2}$ ; -1,5; 2; 3 trên trục số.

Vận dụng 2: Không cần vẽ hình, hãy nêu nhận xét về vị trí của hai số $-\sqrt{2}$ ; $\frac{3}{2}$
Hướng dẫn giải:
Nhận xét về vị trí của hai số $\sqrt{2}$ ; $\frac{3}{2}$ :
$\frac{3}{2}$ = 1,5 ; $\sqrt{2}$ = 1,4142..
Có: $\sqrt{2}$ = 1,4142.. < $\frac{3}{2}$ = 1,5
=> $\sqrt{2}$ nằm bên trái số $\frac{3}{2}$
4. SỐ ĐỐI CỦA MỘT SỐ THỰC
Hoạt động khám phá 4:

Gọi A và A' lần lượt là hai điểm biểu diễn hai số 4,5 và -4,5 trên trục số. So sánh OA và OA'.
Hướng dẫn giải:
Có: OA = 4,5 và OA’=4,5 => OA=OA’.
Thực hành 4: Tìm số đối của các số thực sau: 5,12 ; π ; $-\sqrt{13}$
Hướng dẫn giải:
Số đối của các số thực 5,12 ; π ; $-\sqrt{13}$ lần lượt là: -5,12 ; -π ; $\sqrt{13}$
Vận dụng 3: So sánh các số đối của hai số $-\sqrt{2}$ và $-\sqrt{3}$
Hướng dẫn giải:
Các số đối của hai số $\sqrt{2}$ và $\sqrt{3}$ lần lượt là: $-\sqrt{2}$ và $-\sqrt{3}$.
Do 2 < 3 => $\sqrt{2}$ < $\sqrt{3}$ => $-\sqrt{2}$ > $-\sqrt{3}$.
5. GIÁ TRỊ TUYỆT ĐỐI CỦA MỘT SỐ THỰC
Hoạt động khám phá 5: Trên trục số, so sánh khoảng cách từ điểm 0 đến hai điểm $\sqrt{2}$ và $-\sqrt{2}$
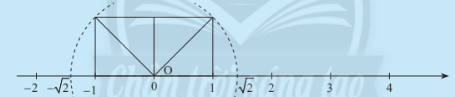
Hướng dẫn giải:
- Khoảng cách từ 0 đến điểm $\sqrt{2}$ là $\sqrt{2}$
- Khoảng cách từ 0 đến điểm $-\sqrt{2}$ là $\sqrt{2}$
=> Khoảng cách từ 0 đến hai điểm $\sqrt{2}$ và $-\sqrt{2}$.
Thực hành 5: Tìm giá trị tuyệt đối của các số thực sau: -3,14; 41; -5; 1,(2); $-\sqrt{5}$.
Hướng dẫn giải:
$ \left| -3,14 \right|=3,14$
$ \left| 41 \right|=41$
$ \left| -5 \right|=5$
$ \left| 1,(2) \right|=1,(2)$
$ \left| -\sqrt{5} \right|=\sqrt{5}$
Vận dụng 4: Có bao nhiêu số thực x thỏa mãn $\left| x \right|=\sqrt{3}$ ?
Hướng dẫn giải:
$\left| x \right|=\sqrt{3}$
=> $x=\sqrt{3}$ hoặc $x=-\sqrt{3}$
Nội dung mở rộng của hướng dẫn giải Toán lớp 7 Chân Trời Sáng Tạo chương trình mới với nhiều dạng Toán 7 nâng cao kì 2, kì 1. Đây chắc chắn là bộ tài liệu quý giúp các em học sinh giành điểm 10 trọn vẹn.
Hướng dẫn giải Toán lớp 7 chương trình mới sách Chân Trời Sáng Tạo sẽ giúp các em học sinh nắm chắc kiến thức trọng tâm, các vị phụ huynh dễ dàng nắm bắt nội dung học và hướng dẫn con làm bài tập. Đừng quên tham khảo thêm nhiều đề thi Toán 7 học kì 2, học kì 2 và bộ câu hỏi trắc nghiệm Toán 7 hữu ích khác được Giaibaitapsgk tổng hợp. Chúc các em học tốt!
