Giải SBT Vật lí 10 Kết nối bài 9 Chuyển động thẳng biến đổi đều
Lời giải bài tập sách 10 Kết Nối Tri Thức của Trang tài liệu được chi tiết theo từng bài nhạc, từng chủ đề. Cùng với đó là hướng dẫn giải Ôn tập cuối năm môn 10 giúp các em hệ thống lại kiến thức đã học trong năm hiệu quả. Sử dụng tài liệu giải bài tập Vật lí của Giaibaitapsgk sẽ giúp các em có thêm nhiều khám phá thú vị với môn học năng khiếu này.
Hướng dẫn giải bài 9: Chuyển động thẳng biến đổi đều SBT vật lí 10. Đây là vở bài tập nằm trong bộ sách "Kết nối tri thức" được biên soạn theo chương trình đổi mới của Bộ giáo dục. Hi vọng, với cách hướng dẫn cụ thể và giải chi tiết học sinh sẽ nắm bài học tốt hơn.
9.1 Chuyển động nào sau đây không phải là chuyển động thẳng biến đổi đều?
A. Viên bi lăn xuống trên máng nghiêng.
B. Vật rơi từ trên cao xuống đất.
C. Hòn đá bị ném theo phương nằm ngang.
D. Quả bóng được ném lên theo phương thẳng đứng.
Đáp án C
- A – chuyển động thẳng nhanh dần đều
- B – chuyển động thẳng nhanh dần đều, cụ thể là sự rơi tự do
- C – chuyển động ném ngang là chuyển động cong.
- D – chuyển động thẳng chậm dần đều.
9.2 Công thức liên hệ giữa độ dịch chuyển, vận tốc và gia tốc của chuyển động nhanh dần đều là
A. $v^{2}-v_{o}^{2}=ad$
B. $v^{2}-v_{o}^{2}=2ad$
C. $v-v_{o}=2ad$
D. $v_{o}^{2}-v^{2}=2ad$
Đáp án B
Công thức liên hệ giữa độ dịch chuyển, vận tốc và gia tốc của chuyển động nhanh dần đều là: $v^{2}-v_{o}^{2}=2ad$
9.3 Đồ thị nào sau đây là của chuyển động thẳng chậm dần đều?
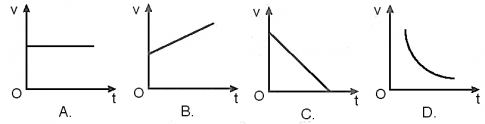
Đáp án C
- A – chuyển động thẳng đều.
- B – chuyển động thẳng nhanh dần đều vì đồ thị có vận tốc tăng đều, độ dốc dương.
- C – chuyển động thẳng chậm dần đều vì đồ thị có vận tốc giảm đều, độ dốc âm.
- D – không phải chuyển động thẳng.
9.4 Chuyển động thẳng chậm dần đều có tính chất nào sau đây?
A. Độ dịch chuyển giảm đều theo thời gian.
B. Vận tốc giảm đều theo thời gian.
C. Gia tốc giảm đều theo thời gian.
D. Cả 3 tính chất trên.
Đáp án B
Chuyển động thẳng chậm dần đều là chuyển động có vận tốc giảm đều theo thời gian.
9.5
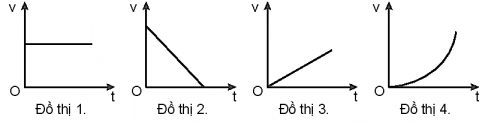
Các chuyển động sau đây có thể phù hợp với đồ thị nào trong bốn đồ thị trên?
a) Chuyển động của ô tô khi thấy đèn giao thông chuyển sang màu đỏ.
b) Chuyển động của vận động viên bơi lội khi có tín hiệu xuất phát.
c) Chuyển động của vận động viên bơi lội khi bơi đều.
d) Chuyển động của xe máy đang đứng yên khi người lái xe vừa tăng ga.
a) Đồ thị 2: vì đồ thị có độ dốc âm thể hiện xe phải chuyển động chậm dần và dừng lại.
b) Đồ thị 3: vì đồ thị có độ dốc dương thể hiện vận động viên phải tăng tốc, vận tốc tăng đều theo thời gian.
c) Đồ thị 1: vì đồ thị có tốc độ chuyển động không đổi theo thời gian nên là chuyển động thẳng đều.
d) Đồ thị 4: vì vận tốc tăng đột ngột không đều.
9.6 Hình 9.1 là đồ thị vận tốc - thời gian của ba chuyển động thẳng biến đổi đều.
a) Viết công thức tính vận tốc và độ dịch chuyển của mỗi chuyển động.
b) Tính độ dịch chuyển của chuyển động (III).
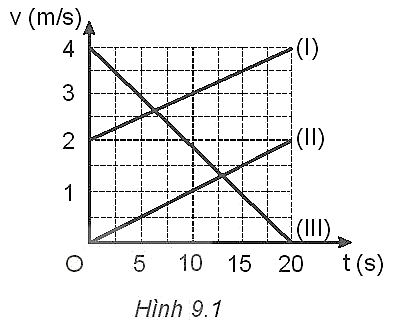
a) Áp dụng:
- Biểu thức tính vận tốc: $v=v_{o}+at$
- Biểu thức tính độ dịch chuyển: $d=v_{o}t+\frac{1}{2}at^{2}$
Vật 1: gia tốc = độ dốc của đồ thị = $a_{1}=\frac{\Delta v_{1}}{\Delta t_{1}}=\frac{4-2}{20-0}=0,1m/s^{2}$
$v_{1}=v_{o}+a_{1}t=2+0,1t$
$d_{1}=v_{o}t+\frac{1}{2}a_{1}t^{2}=2t+0,05t^{2}$
Vật 2: $a_{2}=\frac{\Delta v_{2}}{\Delta t_{2}}=\frac{2-0}{20-0}=0,1m/s^{2}$
$v_{2}=a_{2}t=0,1t$
$d_{2}=\frac{1}{2}a_{2}t^{2}=0,05t^{2}$
Vật 3: $a_{3}=\frac{\Delta v_{3}}{\Delta t_{3}}=\frac{004}{20-0}=-0,2m/s^{2}$
$v_{3}=v_{o3}+a_{3}t=4-0,2t$
$d_{3}=v_{o3}t+\frac{1}{2}a_{3}t^{2}=4t-0,1t^{2}$
b) Độ dịch chuyển của chuyển động (III):
$d_{3}=4t-0,1t^{2}=4.20-0,1.20^{2}$ = 40 m.
9.7 Một máy bay có vận tốc khi tiếp đất là 100 m/s. Để giảm vận tốc sau khi tiếp đất, máy bay chỉ có thể có gia tốc đạt độ lớn cực đại là 4 m/s$^{2}$?
a) Tính thời gian ngắn nhất để máy bay dừng hẳn kể từ khi tiếp đất.
b) Máy bay này có thể hạ cánh an toàn ở sân bay có đường bay dài 1 km hay không?
a) Ta có: $v_{o}$ = 100 m/s; a = -4 m/s$^{2}$
Thời gian ngắn nhất để máy bay dừng hẳn kể từ khi tiếp đất (v = 0) là
$v=v_{o}+at\Rightarrow t=\frac{v-v_{o}}{a}$ = 25 s
b) Quãng đường hạ cánh an toàn của máy bay trong khoảng thời gian ngắn nhất có thể dừng hẳn là:
$d=v_{o}t+\frac{1}{2}at^{2}=100.25+\frac{1}{2}.(-4).25^{2}$ = 1250 m = 1,25 km
Vậy 1 km < 1,25 km nên máy bay không thể hạ cánh an toàn trên sân bay có đường bay dài 1 km
9.8 Một ô tô khi hãm phanh có thể có gia tốc 3 m/s$^{2}$ Hỏi khi ô tô đang chạy với vận tốc là 72 km/h thì phải hãm phanh cách vật cản là bao nhiêu mét để không đâm vào vật cản? Thời gian hãm phanh là bao nhiêu?
Đổi 72 km/h = 72.$\frac{1000}{3600}$ = 20 m/s
Khi hãm phanh, xe chuyển động chậm dần, a và v ngược dấu nhau.
Quãng đường xe dịch chuyển từ khi hãm phanh tới lúc dừng lại là:
Ta có: $v^{2}-v_{o}^{2}=2ad$
$\Rightarrow d=\frac{v^{2}-v_{o}^{2}}{2a}=\frac{0^{2}-20^{2}}{2.(-3)}\approx 66,7m$
Vậy xe phải hãm phanh trước vật cản trên 66,7 m.
Thời gian hãm phanh là
$v=v_{o}+at\Rightarrow t=\frac{v-v_{o}}{a}=\frac{0-20}{-3}\approx 6,7s$
9.9 Một người đi xe máy trên một đoạn đường thẳng muốn đạt được vận tốc 36 km/h sau khi đi được 100 m bằng một trong hai cách sau:
Cách 1: Chạy thẳng nhanh dần đều trong suốt quãng đường.
Cách 2: Chỉ cho xe chạy nhanh dần đều trên $\frac{1}{5}$ quãng đường, sau đó cho xe chuyển động thẳng đều trên quãng đường còn lại.
a) Hỏi cách nào mất ít thời gian hơn?
b) Hãy tìm một cách khác để giải bài toán này.
a) Đổi 36 km/h = 10 m/s.
Cách 1: Vì $v_{o}$ = 0; v = 10 m/s; d = 100 m nên gia tốc của xe trong chuyển động là $a=\frac{v^{2}-v_{o}^{2}}{2d}$
Thời gian xe chuyển động để đạt được 36 km/h trong 100 m là
Từ $v=v_{o}+at\Rightarrow $ t = 20 s (1)
Cách 2: Vì $v_{o}$ = 0; v = 10 m/s; d = $\frac{100}{5}$ = 20 m nên gia tốc trong chuyển động này là $a_{1}=\frac{v^{2}-v_{o}^{2}}{2d_{1}}$
Thời gian chuyển động trong quãng đường này là:
$t_{1}=\frac{v-v_{o}}{a}=\frac{10-0}{2,5}$ = 4 s
Thời gian chuyển động đều trên quãng đường còn lại 100 – 20 = 80 m là:
$t_{2}=\frac{d_{2}}{v}=\frac{80}{10}$ = 8 s
Thời gian chuyển động trong cách 2:
$t=t_{1}+t_{2}$ = 12 s (2)
Từ (1) và (2) ta thấy 12 s < 20 s.
Vậy cách 2 mất ít thời gian hơn.
b) Có thể giải bằng cách tính vận tốc trung bình.
Cách 1: Vận tốc trung bình của chuyển động là
$v_{tb1}=\frac{v+v_{o}}{2}=\frac{0+10}{2}$ = 5 m/s
Thời gian xe chuyển động là $\frac{s}{v_{tb1}}=\frac{100}{5}$ = 20 s (3)
Cách 2:
Vận tốc trung bình của chuyển động trong quãng đường 20 m chuyển động nhanh dần đều là $v_{tb2}=\frac{v+v_{o}}{2}=\frac{0+10}{2}$ = 5 m/s
Thời gian xe chuyển động nhanh dần đều là $t_{1}=\frac{s}{v_{tb2}}=\frac{20}{5}$ = 4 s
Thời gian chuyển động đều trên quãng đường còn lại 100 – 20 = 80 m là: $t_{2}=\frac{d_{2}}{v}=\frac{80}{10}$ = 8 s
Thời gian chuyển động trong cách 2:
$t=t_{1}+t_{2}$ = 12 s (2)
Từ (1) và (2) ta thấy 12 s < 20 s.
Vậy cách 2 mất ít thời gian hơn.
9.10 Một xe đạp đang đi với vận tốc 2 m/s thì xuống dốc chuyển động nhanh dần đều với gia tốc 0,2 m/s$^{2}$. Cùng lúc đó, một ô tô đang chạy với vận tốc 20 m/s lên dốc, chuyển động chậm dần đều với gia tốc 0,4 m/s$^{2}$. Xác định vị trí hai xe gặp nhau trên dốc. Biết dốc dài 570 m.

Chọn chiều từ chân dốc lên đỉnh dốc là chiều dương. Điểm O là chân dốc.
Chuyển động của ô tô: $v_{o1}$ = 20 m/s; $a_{1}$ = -0,4 m/s$^{2}$
Phương trình chuyển động: $d_{1}=20t-0,2t^{2}$ (1)
Chuyển động của xe đạp: $v_{o1}$ = -2 m/s; $d_{o2}$ = 570 m; $a_{2}$ = -0,2 m/s$^{2}$
(vì chuyển động nhanh dần đều thì a.v > 0)
Phương trình chuyển động: $d_{2}=570-2t-0,1t^{2}$ (2)
Khi ô tô và xe đạp gặp nhau:
$d_{1}=d_{2}\Rightarrow 20t-0,2t^{2}=570-2t-0,1t^{2}$ (3)
Nghiệm của phương trình (3) là t$_{1}$ = 30 s và t$_{2}$ = 190 s.
Thay t$_{1}$ vào (1), tính được d$_{1}$ = 420 m (nhận).
Thay t$_{2}$ vào (1), tính được d$_{2}$ = -3420 m (loại vì hai xe gặp nhau trên dốc).
Vị trí hai xe gặp nhau cách chân dốc 420 m.
9.11 Hai vật A và B chuyển động cùng chiều trên đường thẳng có đồ thị vận tốc - thời gian vẽ ở Hình 9.2. Biết ban đầu hai vật cách nhau 78 m.
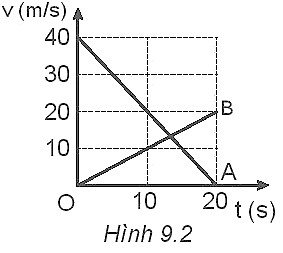
a) Hai vật có cùng vận tốc ở thời điểm nào?
b) Viết phương trình chuyển động của mỗi vật.
c) Xác định vị trí gặp nhau của hai vật.

a) Xét vật A: $a_{A}=\frac{\Delta v_{A}}{\Delta t}=\frac{0-40}{20-0}=-2m/s^{2}$
Phương trình vận tốc của vật A: $v_{A}=40-2t$ m/s
Xét vật B: $a_{B}=\frac{\Delta v_{B}}{\Delta t}=\frac{20-0}{20-0}=1m/s^{2}$
Phương trình vận tốc của vật B: $v_{B}=t$ m/s
Hai vật có cùng vận tốc khi:
$v_{A}=v_{B}\Leftrightarrow 40-2t=t\Rightarrow t=13,3s$
Vậy hai vật có cùng vận tốc tại thời điểm .
b) Chọn trục tọa độ có phương trùng với phương chuyển động của hai vật.
Gốc tọa độ tại vị trí xuất phát của vật A.
Mốc thời gian trùng với thời điểm xuất phát của hai vật.
Chuyển động của vật $d_{A}=v_{oA}t+\frac{1}{2}a_{A}t^{2}=40t-t^{2}$ (1)
Chuyển động của vật $d_{B}=d_{o}+v_{oB}t+\frac{1}{2}a_{B}t^{2}=78+0,5^{2}$ (2)
c) Hai vật gặp nhau khi $d_{A}=d_{B}$
$\Rightarrow 40t-t^{2}=78+0,5^{2}$ (3)
Phương trình (3) cho hai nghiệm t = 2,12 s và t’ = 24,5 s (loại vì t’ > 20 s)
Thay t vào (1) ta được d$_{1}$ = 80,3 m.
Hai vật gặp nhau cách vị trí ban đầu của A là 80,3 m.
9.12 Đồ thị vận tốc - thời gian trong Hình 9.3 là của một xe bus và một xe máy chạy cùng chiều trên một đường thẳng. Xe bus đang đứng yên, bắt đầu chuyển động thì xe máy đi tới.
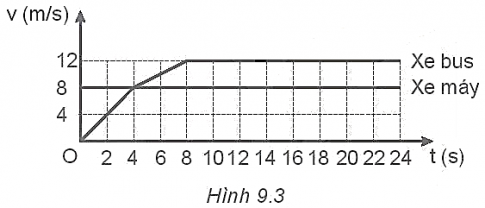
a) Tính gia tốc của xe bus trong 4 s đầu và trong 4 s tiếp theo.
b) Khi nào thì xe bus bắt đầu chạy nhanh hơn xe máy?
c) Khi nào thì xe bus đuổi kịp xe máy?
d) Xe máy đi được bao nhiêu mét thì bị xe bus đuổi kịp?
e) Tính vận tốc trung bình của xe bus trong 8 s đầu.

a) Gia tốc của xe bus trong 4 s đầu: $a_{1}=\frac{\Delta v_{1}}{\Delta t_{1}}=\frac{8-0}{4-0}=2m/s^{2}$
Gia tốc của xe bus trong 4 s tiếp theo: $a_{2}=\frac{\Delta v_{2}}{\Delta t_{2}}=\frac{12-8}{8-4}=1m/s^{2}$
b) Sau giây thứ 4 thì vận tốc của xe bus lớn hơn vận tốc của xe máy.
c) Dựa vào đồ thị, diện tích hình giới hạn bởi đường biểu diễn trong đồ thị vận tốc - thời gian có độ lớn bằng quãng đường đi được. Khi hai xe gặp nhau, thì diện tích hình giới hạn bởi đường biểu diễn cho hai xe bằng nhau.
Ta thấy diện tích hình chữ nhật OAHI giới hạn bởi đường biểu diễn v – t cho xe máy bằng với diện tích hình OCKLI giới hạn bởi đường biểu diễn v – t cho xe bus cùng bằng 10 ô. Do đó, tại thời điểm t = 10 s thì d$_{1}$ = d$_{2}$, nghĩa là xe bus đuổi kịp xe máy.
Kiểm tra bằng phương trình chuyển động:
Đối với xe bus:
Trong 4 s đầu: $d_{1}=\frac{1}{2}a_{1}t_{1}^{2}=\frac{1}{2}.2.4^{2}=16m$
Trong 4 s tiếp theo: $d_{2}=v_{o}t_{2}+\frac{1}{2}a_{2}t_{2}^{2}=8.4+\frac{1}{2}.1.4^{2}=40m$
Trong các giây tiếp theo: $d_{3}=v_{3}t_{3}=12t_{3}$
Nếu gọi thời điểm hai xe gặp nhau là t thì $t_{3}=t\pm (t_{1}+t_{2})\Rightarrow t_{3}=t\pm 8$
Chọn dấu “-” vì trong 8 s đầu xe bus mới đi được d$_{1}$ + d$_{2}$ = 56 m, còn xe máy đã đi được $d_{m}=v_{m}t_{m}=8.8=64m>56m$
Độ dịch chuyển của xe máy trong thời gian t là $d_{m}=v_{m}t=8t$ (1)
Độ dịch chuyển của xe bus trong thời gian t là
$d_{b}$ = 16 + 40 + 12$t_{3}$ = 16 + 40 + 12(t - 8) = 12t - 40 (2)
Khi hai xe gặp nhau $d_{m}=d_{b}\Rightarrow $ 12t - 40 = 8t $\Rightarrow $ t = 10s
Hai xe gặp nhau tại thời điểm t = 10 s.
d) Khi đó xe máy chạy được $d_{m}=v_{m}t=8t=8.10=80m$
e) Vận tốc trung bình của xe bus trong 8 s đầu
$v_{tb}=\frac{d_{1}+d_{2}}{t_{1}+t_{2}}=\frac{16+40}{8}$ = 7 m/s
Xem thêm ôn tập cuối kì môn 10 kèm lời giải bài tập sách 10 Kết Nối Tri Thức chi tiết. Luyện tập theo đề cương giúp các em nắm bắt kiến thức trọng tâm và hoàn thiện những kỹ năng, sẵn sàng cho kì thi sắp tới.
Mong rằng đáp án và lời giải bài tập sách 10 Kết Nối Tri Thức sẽ mở ra cánh cửa mới giúp các em tìm thấy niềm vui khi học âm nhạc. Đồng thời cũng khám phá thêm nhiều kiến thức mới hữu ích để có thể vận dụng linh hoạt vào cuộc sống. Chúc các em học tập tốt và đạt điểm số cao trong những kì thi sắp tới.
