Giải SBT Vật lí 10 Kết nối bài 13 Tổng hợp và phân tích lực. Cân bằng lực
Lời giải bài tập sách 10 Kết Nối Tri Thức của Trang tài liệu được chi tiết theo từng bài nhạc, từng chủ đề. Cùng với đó là hướng dẫn giải Ôn tập cuối năm môn 10 giúp các em hệ thống lại kiến thức đã học trong năm hiệu quả. Sử dụng tài liệu giải bài tập Vật lí của Giaibaitapsgk sẽ giúp các em có thêm nhiều khám phá thú vị với môn học năng khiếu này.
Hướng dẫn giải bài 13: Tổng hợp và phân tích lực. Cân bằng lực SBT vật lí 10. Đây là vở bài tập nằm trong bộ sách "Kết nối tri thức" được biên soạn theo chương trình đổi mới của Bộ giáo dục. Hi vọng, với cách hướng dẫn cụ thể và giải chi tiết học sinh sẽ nắm bài học tốt hơn.
13.1 Một chất điểm chịu tác dụng đồng thời của hai lực $\vec{F_{1}}$ và $\vec{F_{2}}$ thì hợp lực $\vec{F}$ của chúng luôn có độ lớn thoả mãn hệ thức
A. F = F1 – F2.
B. F = F1 + F2.
C. | F1 – F2 | ≤ F ≤ F1 + F2.
D. F2 = F12 + F22.
Đáp án C
| F1 - F2 | ≤ F ≤ F1 + F2
13.2 Hợp lực của hai lực $\vec{F_{1}}$ và $\vec{F_{2}}$ hợp với nhau một góc α có độ lớn thoả mãn hệ thức
A. F = F1 + F2.
B. F = F1 – F2.
C. F2 = F12 + F22 – 2F1F2cosα.
D. F2 = F12 + F22 + 2F1F2cosα.
Đáp án D
Ta có vectơ lực tổng hợp: $\vec{F}=\vec{F_{1}}+\vec{F_{2}}$
Độ lớn lực tổng hợp: F = $\sqrt{F_{1}^{2}+F_{2}^{2}+2F_{1}F_{2}cos\alpha }$
=> F2 = F12 + F22 + 2F1F2cosα
13.3 Nếu một chất điểm chuyển động dưới tác dụng của hai lực $\vec{F_{1}}$ và $\vec{F_{2}}$ khác phương, $\vec{F}$ là hợp lực của hai lực đó thì vectơ gia tốc của chất điểm
A. cùng phương, cùng chiều với lực $\vec{F_{1}}$
B, cùng phương, cùng chiều với lực $\vec{F_{2}}$
C. cùng phương, cùng chiều với lực $\vec{F}$
D. cùng phương, ngược chiều với lực $\vec{F}$
Đáp án C
Tổng hợp lực là phép thay thế các lực tác dụng đồng thời vào cùng một vật bằng một lực có tác dụng giống hệt như các lực ấy. Lực thay thế này gọi là hợp lực.
Trong câu này $\vec{F}$ là hợp lực của hai lực $\vec{F_{1}}$ và $\vec{F_{2}}$ khác phương nên vectơ gia tốc của chất điểm sẽ cùng phương, cùng chiều với lực $\vec{F}$ .
13.4 Một chất điểm chịu tác dụng của một lực $\vec{F}$ có độ lớn là 20 N. Nếu hai lực thành phần của lực đó vuông góc với nhau có độ lớn lần lượt là F1 = 12 N và F2 thì F2 bằng
A. 8N.
B. 16 N.
C. 32 N
D. 20 N.
Đáp án B
Ta có: $\vec{F_{1}}\perp \vec{F_{2}}\Rightarrow F=\sqrt{F_{1}^{2}+F_{2}^{2}}$
=> F2 = F12 + F22 = => F2 = $\sqrt{F^{2}-F_{1}^{2}}=\sqrt{20^{2}-12^{2}}$ = 16 N.
13.5 Hai lực có giá đồng quy có độ lớn là 6 N và 8 N và có phương vuông góc với nhau. Hợp lực của hai lực này có độ lớn là
A. 4N.
B. 10 N.
C. 2 N.
D. 48 N
Đáp án B
Ta có: $\vec{F_{1}}\perp \vec{F_{2}}\Rightarrow F=\sqrt{F_{1}^{2}+F_{2}^{2}}=\sqrt{6^{2}+8^{2}}$ = 10 N.
13.6 Hai lực khác phương $\vec{F_{1}}$ và $\vec{F_{2}}$ có độ lớn F1 = F2 = 20 N, góc tạo bởi hai lực này là 60$^{o}$. Hợp lực của hai lực này có độ lớn là
A. 14,1 N.
B. 20$\sqrt{3}$ N.
C. 17,3 N.
D. 20 N.
Đáp án B
Ta có: F = $\sqrt{F_{1}^{2}+F_{2}^{2}+2F_{1}F_{2}cos\alpha }=\sqrt{20^{2}+20^{2}+2.20.20.cos60^{o}}=20\sqrt{3}$ N
13.7 Hai lực khác phương có độ lớn bằng 9 N và 12 N. Hợp lực của hai lực này không thể có độ lớn nào sau đây?
A. 2 N.
B. 15 N.
C. 11,1 N.
D. 21 N.
Đáp án A
Ta có: |F1 – F2| ≤ F ≤ F1 + F2 => 3 N ≤ F ≤ 21 N.
=> Hợp lực của hai lực này không thể có độ lớn là 2 N.
13.8 Một chất điểm chịu tác dụng của hai lực có độ lớn 18 N và 24 N. Biết hợp lực của hai lực này có giá trị 30 N, góc tạo bởi hai lực này là
A. 90°.
B. 30°.
C. 45°.
D. 60°.
Đáp án A
Ta có độ lớn của lực tổng hợp được tính bằng công thức:
$F=\sqrt{F_{1}^{2}+F_{2}^{2}+2F_{1}F_{2}cos\alpha }$
$\Rightarrow cos\alpha =\frac{F^{2}-F_{1}^{2}-F_{2}^{2}}{2F_{1}F_{2}}=\frac{30^{2}-24^{2}-18^{2}}{2.24.18}=0$
$\Rightarrow \alpha =90^{o}$
13.9 Một chất điểm chịu tác dụng của ba lực $\vec{F_{1}},\vec{F_{2}},\vec{F_{3}}$có cùng độ lớn 12 N. Biết góc tạo bởi các lực $(\vec{F_{1}},\vec{F_{2}})$ = $(\vec{F_{2}},\vec{F_{3}})$ = 60$^{o}$ (Hình 13.1). Hợp lực của ba lực này có độ lớn là
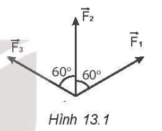
A. 6 N.
B. 24 N.
C. 10,4 N.
D. 20,8 N.
Đáp án B

Hợp lực: $\vec{F}=\vec{F_{1}}+\vec{F_{2}}+\vec{F_{3}}=\vec{F_{13}}+\vec{F_{2}}$
Theo quy tắc hình bình hành và kết hợp với điều kiện ba lực $\vec{F_{1}},\vec{F_{2}},\vec{F_{3}}$ có độ lớn bằng nhau => Hình bình hành thành hình thoi nên hợp lực của $\vec{F_{1}}$ và $\vec{F_{3}}$ cùng phương, cùng chiều với lực $\vec{F_{2}}$ nên độ lớn hợp lực của ba lực trên là:
F = F13 + F2 hay F = $\sqrt{F_{1}^{2}+F_{3}^{2}+2F_{1}F_{3}cos120^{o}}$ + F2 = 24 N.
13.10 Một con nhện đang treo mình dưới một sợi tơ theo phương thẳng đứng thì bị một cơn gió thổi theo phương ngang làm dây treo lệch đi so với phương thẳng đứng một góc 30°. Biết trọng lượng của con nhện là P = 0,1 N. Xác định độ lớn của lực mà gió tác dụng lên con nhện ở vị trí cân bằng trong Hình 13.2.
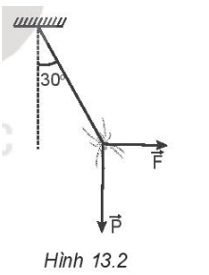
Khi con nhện và sợi tơ cân bằng như hình vẽ:

Ta có: tan30o = $\frac{F}{P}$
=> F = Ptan30o = $\frac{0,1}{\sqrt{3}}\approx 0,058$ N.
13.11 Một vật chịu tác dụng đồng thời của bồn lực như Hình 13.3. Độ lớn của các lực lần lượt là F1 = 10 N, F2 = 20 N, F3 = 22 N, F4 = 36 N. Xác định phương, chiều và độ lớn của hợp lực do các lực này tác dụng lên vật.
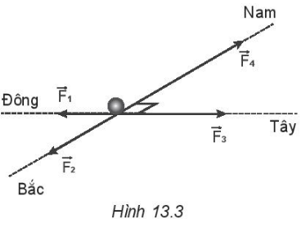
Hợp lực: $\vec{F}=\vec{F_{1}}+\vec{F_{2}}+\vec{F_{3}}+\vec{F_{4}}=\vec{F_{13}}+\vec{F_{24}}$

Vì $\vec{F_{1}}$ ↑↓ $\vec{F_{3}}$ => F13 = |F1 – F3| = 12 N
F1 < F3 => F13 cùng phương F3 và có chiều từ Đông sang Tây.
Và $\vec{F_{2}}$ ↑↓ $\vec{F_{4}}$ => F24 = |F2 – F4| = 16 N
F2 < F4 => F24 cùng phương F4và có chiều từ Bắc sang Nam.
Khi đó ta có thể thấy: $\vec{F_{13}}\perp \vec{F_{24}}$
Độ lớn hợp lực là:
$F=\sqrt{F_{13}^{2}+F_{24}^{2}}=\sqrt{12^{2}+16^{2}}$ = 20 N.
Vậy hợp lực F có phương và chiều như hình vẽ, độ lớn F = 20 N.
13.12 Một cái đèn được treo vào hai sợi dây giống nhau như Hình 13.4. Biết trọng lượng của đèn là 25 N, hai dây làm thành góc 60°. Xác định lực căng của dây.
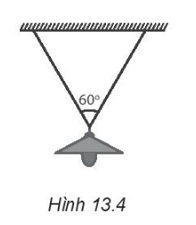
Khi đèn và dây treo cân bằng, các lực tác dụng lên đèn được biểu diễn như hình vẽ.

Theo hình vẽ ta có phương trình cân bằng lực:
$\vec{T_{1}}+\vec{T_{2}}+\vec{P}=\vec{0}\Rightarrow \vec{T_{1}}+\vec{T_{2}}=-\vec{P}$
Mà về độ lớn: T1 = T2 = T=> P = 2Tcos30$^{o}$
T = $\frac{P}{\sqrt{3}}=\frac{25}{\sqrt{3}}$ ≈ 14,4 N.
Vậy lực căng dây T có cùng phương, ngược chiều với P như hình vẽ và có độ lớn T ≈ 14,4 N.
Xem thêm ôn tập cuối kì môn 10 kèm lời giải bài tập sách 10 Kết Nối Tri Thức chi tiết. Luyện tập theo đề cương giúp các em nắm bắt kiến thức trọng tâm và hoàn thiện những kỹ năng, sẵn sàng cho kì thi sắp tới.
Mong rằng đáp án và lời giải bài tập sách 10 Kết Nối Tri Thức sẽ mở ra cánh cửa mới giúp các em tìm thấy niềm vui khi học âm nhạc. Đồng thời cũng khám phá thêm nhiều kiến thức mới hữu ích để có thể vận dụng linh hoạt vào cuộc sống. Chúc các em học tập tốt và đạt điểm số cao trong những kì thi sắp tới.
